SudokuWiki.org
Strategies for Popular Number Puzzles
Aligned Pair Exclusion
This is an interesting strategy, known by the short-hand as APE and sometimes called Subset Exclusion. It can overlap with Y-Wings, XYZ-Wings and WXYZ-Wings but uses very different logic. The overlap is not strict so they are worth looking out for in a tough situation.
There is always a base pair of cells (which now show up as grey cell on the solver). At least one elimination will occur in one of those two cells. The solver will also show a variety of colored cells which are the elements used to make an elimination. I used to distinguish between APE type 1 which only used bi-value cells and type 2 which used 2-cell Almost Locked Sets (ALSs). But the solver will now find a larger variety including 3-cell ALSs and since these merely extend the same logic the solver will return the first of any it finds. A better Type 1 and Type 2 distinction is between the base pair of cells which can be a locked pair (ie can see each other) or not (can't see each other). The logic is subtly different but I'll come to this in the following examples.
There is always a base pair of cells (which now show up as grey cell on the solver). At least one elimination will occur in one of those two cells. The solver will also show a variety of colored cells which are the elements used to make an elimination. I used to distinguish between APE type 1 which only used bi-value cells and type 2 which used 2-cell Almost Locked Sets (ALSs). But the solver will now find a larger variety including 3-cell ALSs and since these merely extend the same logic the solver will return the first of any it finds. A better Type 1 and Type 2 distinction is between the base pair of cells which can be a locked pair (ie can see each other) or not (can't see each other). The logic is subtly different but I'll come to this in the following examples.
Aligned Pair Exclusion - Type 1
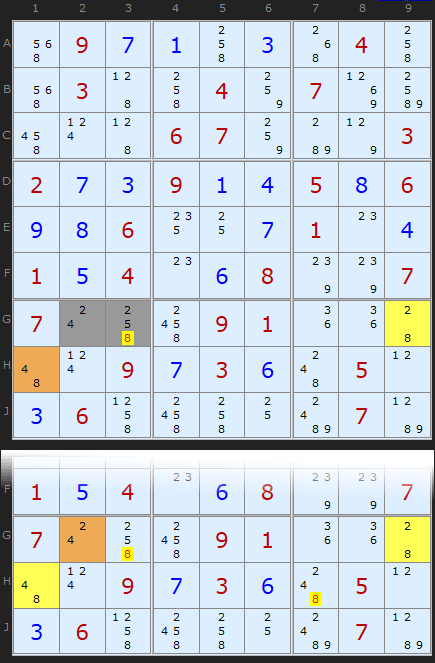
(requires Y-Wing unchecked) : Load Example or : From the Start
The Aligned Pair Exclusion can be succinctly stated: Any two cells that can see each other CANNOT duplicate the contents of any Almost Locked Set they both entirely see and share candidates with.
Remember - a bi-value cell (with two candidates) is the simplest Almost Locked Set since it is a set of size '1' with size+1 (ie two) candidates.
Let's consider the simplest possible example - two bi-value cell attacking the pair. I have also shown the Y-Wing in the diagram so we can see there is a simpler way to do the same job - but only in some cases.
We consider ALL the possible pairs of numbers that will fit in [G2/G3]. These are for G2 and G3:
2 and 5
2 and 8
4 and 2
4 and 5
4 and 8
Apart from the first being impossible (2 and 2) since G2 and G3 can see each other, we have problems with some of the other combinations. What if 2 and 8 were tried as the solutions? Well, that would duplicate and therefore empty G9. Also 4 and 8 would empty H1.
We are left with a set of combinations that looks like this:
2 and 2 (impossible)
2 and 5
2 and 8 (impossible)
4 and 2
4 and 5
4 and 8 (impossible)
Notice that we now have no 8 left in any pairing? Therefore we can remove 8 from our base pair. Voilà
Credits - Rod Hagglund first popularised this method. (links now dead).
2 and 5
4 and 2
4 and 5
Notice that we now have no 8 left in any pairing? Therefore we can remove 8 from our base pair. Voilà
Credits - Rod Hagglund first popularised this method. (links now dead).
Example 2
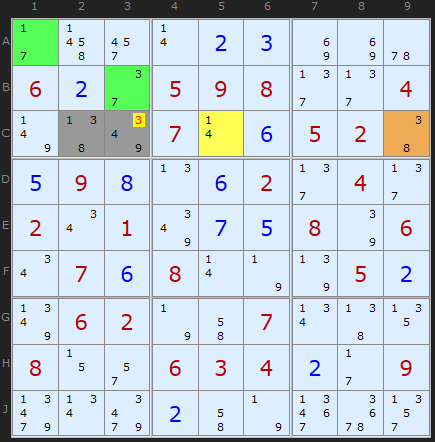
The 2-cell ALS in [A1,B3] contains {1/3/7} so pairs that would cripple the solution for that ALS are {1,3}, {1,7} and {3,7}.
Let's consider all the possible pairs of numbers in our base pair [C2/C3]. These are:
1 and 9
3 and 4
3 and 9
8 and 4
8 and 9
Now, we have to be a tiny bit careful here. 3 has definitely been excluded as a possible solution in C3 but look down the list and 3 + 4 is still OK and 3 + 9 is OK. So we can't remove 3 from C2 just yet.
Credits: Myth Jellies came up with the insight for abc = ab/ac/bc
Note: There could be more than two, sometimes three or four ALSs of several sizes in an APE attack. I've considered examples with two for simplicity's sake
Example 3
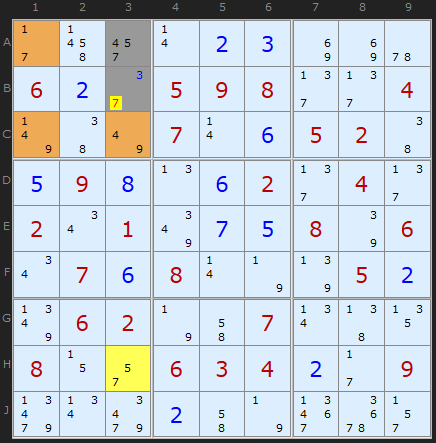
4 and 3
5 and 3
7 and 3
The tricky one with the 3-cell ALS is not the fact that the base pair will empty it (it can't since it is two cells and the ALS is 3 cells). It's the fact that a solution of 4 in A3 and 7 in B3 would mean there'd be only two candidates left to fill three cells. Thats enough to rule out the combination.
Aligned Pair Exclusion - Type 2
Aligned Pair Exclusion can also work even if the pair is not aligned. Sounds like a joke, but it's too late now to rename this strategy :) Perhaps 'Subset Exclusion' was a better idea. There is a subtle logical different but I have found many examples and it boosts the usefulness of this strategy.
I'm very grateful to Joseph Aleardi for putting me on the scent of this elegant logic.
I'm very grateful to Joseph Aleardi for putting me on the scent of this elegant logic.
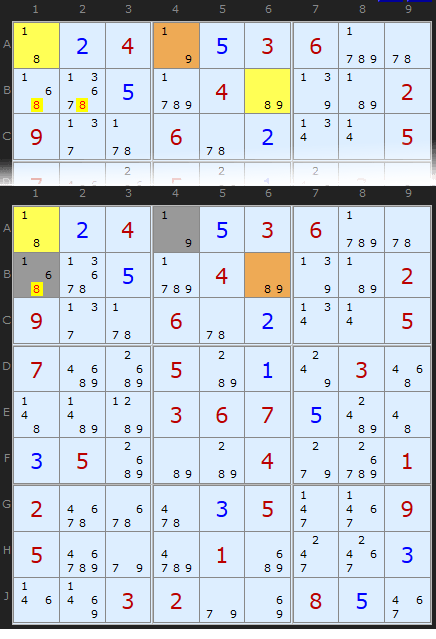
The diagram here shows first the Y-Wing based on A1 - A4 (the pivot) - B6. It's quite easy to see that 8 must occur in either A1 or B6, thus removing it from B1 and B2.
But let's follow the APE logic with the non-aligned pair A4 and B1. (Note: We could also choose A1 and B2 and eliminate the 8 there also). A4 pairs with B1 using these combinations:
1 and 1 - POSSIBLE!
1 and 6
9 and 1
9 and 6
The only difference between APE 1 and APE 2 is that with non-aligned pairs the same candidate *could* be a solution in both cells. So 1 and 1 is definitely on the cards. Not that it is critical in this case. The other exclusions mean we can't have an 8 in B1, just as we thought.
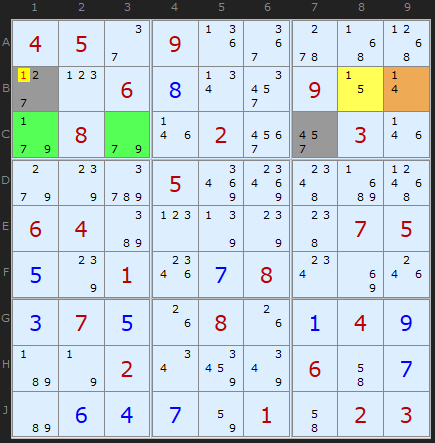
Here is a more complex APE that does not have a Wing alternative. We have two bi-value cells and one two cell ALS attacking B1 and C7. Let's write out the combinations between those cells:
1 and 4 - excluded by B9
1 and 5 - excluded by B8
1 and 7 - excluded by [C1 + C3]
2 and 4
2 and 5
2 and 7
7 and 4
7 and 5
7 and 7 - Permitted!
Clearly 1 is removed from B1. The exact same formation also removes 1 from B2.
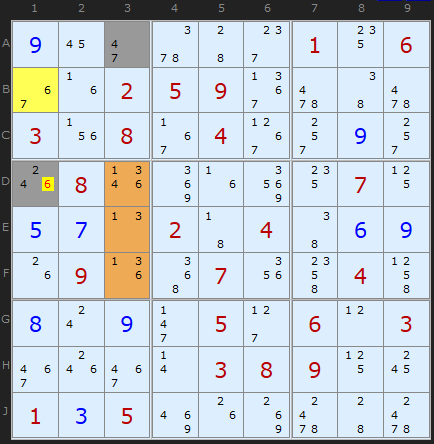
To conclude, a non-aligned pair using a bi-value cell and a 3-cell ALS. I'll leave it to the reader to work out why 6 can be removed from D1.
There is a second very nice APE later in the solving sequence using a 2-cell ALS and a 3-cell ALS. You can load the puzzle from the links under the diagram.
An Eight-Cell Aligned Pair
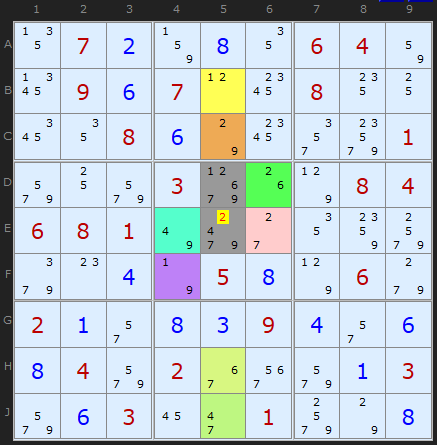
How many difficult puzzles did Klaus have to check to find this? Astonishingly, around 21 million!
Comments
... by: Stefan
... by: S. Lee
Besides the chaining strategies, there is also a family of strategies that make use of the concept of 'wing'. Indeed, the following strategies
XY-Wing
XYZ-Wing
XYZW-Wing
Aligned Pair Exclusion (possibly partially)
Sue-De-Coq (possibly partially)
can be understand as special cases of the strategy named 'Bent-Naked subset' as is illustrated in Sudoku Assistant (http://www.stolaf.edu/people/hansonr/sudoku/explain.htm). This strategy admits two rules as follows:
Setting) Let A and B be a subset of two overlapping units (such as row-box). Let
Wa = [portion of A that does not overlap with B] = A-B
Wb = [portion of B that does not overlap with A] = B-A
U = [union of A and B] = A∪B
so that both Wa and Wb form two wings of U. Assume that U is 'bent-locked', in the sense that the number of candidates on the cells in U is equal to the number of cells in U.
Rule 1) If there is no common candidate between two wings Wa and Wb, then A behaves like a genuine naked subset with candidates of Wa in each unit, and likewise for B.
Rule 2) If there is a unique candidate k between two wings Wa and Wb, then for every cell that can see the candidate k in U, we can eliminate the candidate k from the cell.
The power of this strategy is that we do not care what happens in the intersection part A∩B, except that it affects the total number of the candidate in U = A∪B. Conceptually it involves neither the concept of bi-valued cells nor that of tri-valued cell, though they appear in many examples. Even this does not involve the notion of ALS. All the matter reduces to the problem of candidate counting in U, Wa and Wb.
Of course, the disadvantage of this strategy is that there is no guide for the choice of A and B. Thus it is of no harm to understand that both APE and Sue-De-Coq are special guidelines for choosing the pair (A, B).
In the 1st APE example, we actually have
Wa = {1,2}[F5]
Wb = {2,5,6}[E7|E8]
U = {1,2,5,6}[F5|E7|E8|F9]
Clearly U forms a bent-locked subset. Since there is a unique candidate, namely 2, in both wings Wa and Wb, we can eliminate the candidate 2 in F8 as F8 can see all the candidates 2 in the subset U by the Rule 2.
Other two examples can also be analyzed by exactly the same manner:
Extended APE example 1:
Wa = {5,6,9}[D9|F9]
Wb = {1,9}[G8]
U = {1,5,6,9}[D9|F9|G8|H9]
=> 9 in J9 is eliminated by Rule 2
Wa = {5,6,9}[D9|F9]
Wb = {3,6}[J7]
U = {3,5,6,9}[D9|F9|J7|J9]
=> 6 in H9 is eliminated by Rule 2
Extended APE example 2:
Wa = {1,5,9}[A2|A9]
Wb = {8,9}[B4]
U = {1,5,6,8,9}[A2|A9|B4|A4|A5]
=> 9 in A6 is eliminated by Rule 2
Sue-De-Coq example 1:
Wa = {2,8}[B2]
Wb = {3,5}[F3]
U = {2,3,5,8}[B2|F3|D2|E2]
=> By the Rule 1,
The triple A = [B2|F3|D2] behaves like a naked pair with candidates {2, 8} in column 2, eliminating 8 in C2, 2 in G2 and 8 in J2.
The triple B = [F3|D2|E2] behaves like a naked pair with candidates {3, 5} in box B1, eliminating 3 in E3.
Sue-De-Coq example 2:
Wa = {6,8}[E2]
Wb = {1,3,7}[D9|F9]
U = {1,3,6,8,9}[E2|D9|F9|E7|E8]
=> By the Rule 1,
The triple [E2|E7|E8] behaves like a naked pair with candidates {6,8} in the row E, eliminating 6 and 8 in the other cells in the row E.
The quadraple [D9|F9|E7|E8] behaves like a naked triple with candidates {1,3,7} in the box B3, eliminating 1, 3, 7 in the other cells in the box B3.
In fact, we may extend the bent-naked subset strategy to a more general setting, though it becomes slightly harder to identify, as the naked triple is harder to apply than the naked pair.
... by: Bruce A Rogers