How Sudoku X Breaks Symmetries
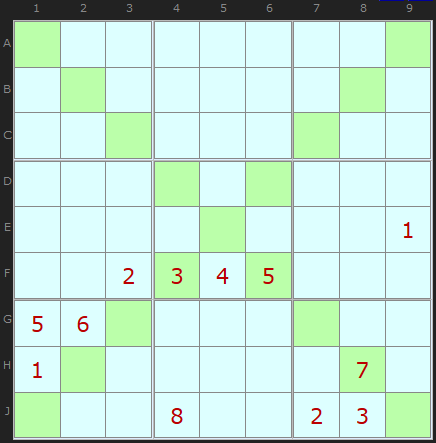
It is an interesting question how a puzzle like the one illustrated here can have one solution. All the clues are stacked in the bottom half of the board with just one number in the middle row in E9. This puzzle is the first in a list of 12 clue puzzles [1]. They are interesting both as very minimal puzzles (minimal clues) and for how they highlight just how different Sudoku X can be from normal Sudoku.
Sudoku X has two extra constraints in the diagonals - which must be filled with 1 to 9. Almost all Sudoku strategies can be applied to X and extended to take advantage of the diagonals as I wrote in this article. There are pitfalls, especially with patterns that require rectangles and specific combinations of rows, boxes and columns, as I also point out.
The number of possible Sudoku puzzles can only be determined by the puzzle creator since they are in charge of how many clues to leave on the puzzle. A better idea of how much choice we have is to look at filled in Sudoku boards, which are the possible solutions. There are an enormous number of ways to fill a Sudoku grid without breaking the puzzles rules. 6,670,903,752,021,072,936,960 to be precise. But this number is misleading. What if I rotate the grid? Does that make it a different puzzle or solution? Only superficially. Any puzzle rotated will solve in the same way as you can check on my solver using the left/right buttons. So this gives us an idea that there must be some smaller number that represents all unique solution grids. Lets list the ways a grid can be changed superficially without actually changing it fundamentally:
These are call the geometric symmetries. There is another way we can mess up a grid:
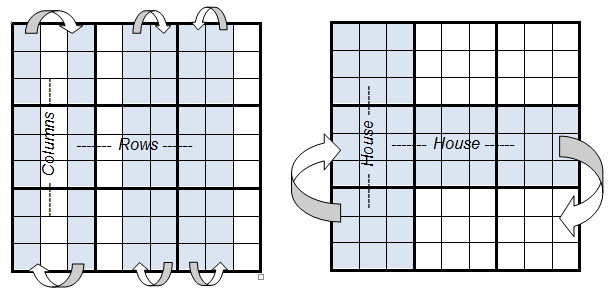
Now, just with normal Sudoku, there are two more symmetries, as illustrated in these diagrams.
This reduces the total number of solution grids to a much more manageable, if still vast, 5,472,730,538.
- Rotation is a symmetry and there are four ways a puzzle can be present by rotation - 0°, 90°, 180° and 270°.
- Reflection. Four ways: One can reflect horizontally or vertically and in both diagonals.
These are call the geometric symmetries. There is another way we can mess up a grid:
- by changing the numbers consistently, for example all 5s will be 4 and all 4s will be 5. The number of ways to renumber a grid is 9! (9 factorial) or 362,880.
Now, just with normal Sudoku, there are two more symmetries, as illustrated in these diagrams.

- Within a 'house' or 'chute' (made from 3x3 boxes) one can swap rows and columns
- Houses or Chutes can themselves be swapped
This reduces the total number of solution grids to a much more manageable, if still vast, 5,472,730,538.
These symmetries have a special effect when it comes to creating a normal Sudoku puzzle. If the top two rows (for example) can be swapped then double or multiple solutions could result. In order to lock down the rows so they can't be swapped, it is necessary to leave some numbers in those rows. You will find many puzzles where all the numbers are missing from one row, but never two or three rows in the same house. Same goes for columns. These ideas feed into strategies like Avoidable Rectangles.
These two types of symmetry are simply not available in Sudoku X. In the diagram below I've taken a Sudoku X grid and swapped the first house with the second house. This messes drastically with the diagonals and although the numbers have moved and still conform to a normal Sudoku puzzle they do not conform to Sudoku X rules.
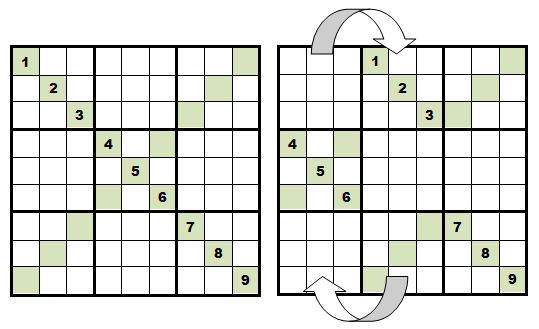
This has several effects.
If these symmetries are not available then the reducing factor to get the number of unique solutions is smaller - but the starting number of total possible solutions is itself much smaller. I'd love to work out or find a reference to what these numbers are exactly. The work of Bertram Felgenhauer and Fraser Jarvis (pdf) has been widely reported but their numbers are for normal Sudoku. I am pretty convinced that the total number of unique solution grids is much less than 5 billion.
Secondly, any new constraint reduces the number of necessary clues. We can see that clearly with the work on 17-clue proofs and the presence of seven thousand odd 12-clue Sudoku X puzzles. More constraints mean more cells being able to see each other. The diagonals in Sudoku X bring previously out of reach territory into mutual contact.
Thirdly, the reach of the diagonals means the overall spread of clues can include highly bunched patterns like the first example. Most published puzzles are symmetrical around the center for aesthetic reasons but these are a small subset of possible puzzles. However, only with Sudoku X can you skip clues across so many rows, columns and boxes.
All this makes these 12 clue puzzles very interesting and pleasing.
These two types of symmetry are simply not available in Sudoku X. In the diagram below I've taken a Sudoku X grid and swapped the first house with the second house. This messes drastically with the diagonals and although the numbers have moved and still conform to a normal Sudoku puzzle they do not conform to Sudoku X rules.

This has several effects.
If these symmetries are not available then the reducing factor to get the number of unique solutions is smaller - but the starting number of total possible solutions is itself much smaller. I'd love to work out or find a reference to what these numbers are exactly. The work of Bertram Felgenhauer and Fraser Jarvis (pdf) has been widely reported but their numbers are for normal Sudoku. I am pretty convinced that the total number of unique solution grids is much less than 5 billion.
Secondly, any new constraint reduces the number of necessary clues. We can see that clearly with the work on 17-clue proofs and the presence of seven thousand odd 12-clue Sudoku X puzzles. More constraints mean more cells being able to see each other. The diagonals in Sudoku X bring previously out of reach territory into mutual contact.
Thirdly, the reach of the diagonals means the overall spread of clues can include highly bunched patterns like the first example. Most published puzzles are symmetrical around the center for aesthetic reasons but these are a small subset of possible puzzles. However, only with Sudoku X can you skip clues across so many rows, columns and boxes.
All this makes these 12 clue puzzles very interesting and pleasing.
1.originally published on sudocue.net at http://www.sudocue.net/sudoku-x-12-7193.sdm, but the page not longer exists

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Leren
http://forum.enjoysudoku.com/sudokux-diagonal-sudoku-t34959-75.html
... by: altikaka
It has a puzzle page each day, and one of the puzzles is called SUDOKUX.
This is a 6 x 6 grid, split into 6 off 3x2 boxes.
The numbers 1 - 6 are used to complete each box and no two equal numbers can be in line either vertically, horizontally or on the two major diagonals. (Diagonals in adjacent boxes are OK).
If you are not familiar with this puzzle then let me know and I'll send a sample.
Regards
David
... by: Leren
The number of different Sudoku X Grids is (9!) * 153,255,603,504
The number of essentially different Sudoku X Grids is 1,596,582,158
These numbers were worked out by the geniuses on the New Sudoku Players Forum at the following address
forum.enjoysudoku.com/sudokux-diagonal-sudoku-t34959.html
The number of known essentially different 12 clue puzzles is now close to 80,000.
To get the number of absolutely different 12 clue puzzles multiply this number by 96 x 9!
No 11 clue puzzle has been found - yet, but we've come close, with two 11 clue sets having just 2 solutions.
I can supply you with a list of all of the known ED 12 clue puzzles if you want.
Cheers
... by: Mark
One of my favourite things about variations of Sudoku like X-Sudoku is that you can have even less clues in a puzzle like the example puzzle you have at the top. I used to solve other variations of Sudoku like Clueless puzzles where there is a puzzle made out of 10 grids, and one of them has no clues at all on it (http://www.sudocue.net/clueless.php). I now do a lot of Picture Sudoku puzzles where you often have no clues at all in the main grid (www.picturesudoku.co.uk).
A common element throughout puzzles that they all break the symmetry, which as you showed results in being able to have a lot less clues.