Simple Colouring
Simple Colouring, also known as Single's Chains is a chaining strategy and part of a large family of such strategies. 'Simple' refers to the idea that one candidate number is considered - in contrast to 'multi-colouring' which is the basis of 3D Medusa. Simple Colouring also related to X-Cycles.
A 'chain' is a series of links hopping from one candidate to another following very simple rules. A candidate can either be ON or OFF. That is, we either think it is a possible solution to that cell, or we do not. There are consequences to the rest of the board when we 'link' these two states. When we are starting out we don't know which will be ON or OFF so any two colours will do.
A 'chain' is a series of links hopping from one candidate to another following very simple rules. A candidate can either be ON or OFF. That is, we either think it is a possible solution to that cell, or we do not. There are consequences to the rest of the board when we 'link' these two states. When we are starting out we don't know which will be ON or OFF so any two colours will do.
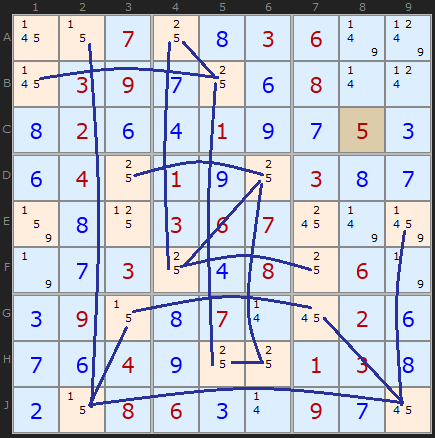
Now, the Colouring aspect which sometimes gives this strategy its name, is illustrated in the rules below. Each end of each link can be assigned one of two colours. You can start in any position, taking any 5 on the board and give it one colour. Then follow each chain link alternating the colour. The strategy is all about recognising that one of those colours will be the solution and the other not. The rules that follow identify the contradictions that allow us to eliminate candidates or decide which colour (which end of every link) is the solution.
Just a note on rule numbers: The solver uses the same search algorithm for both Simple Colouring and 3D Medusa so I have synchronised the rule numbers that are returned. Rules 1 and 3 apply only to 3D Medusa (Multi-colouring) since they extend chains to different numbers. However, the solver needs to look for Simple Colouring first because I deem it to be a simpler strategy that's easier to search for.
Rule 2 - Twice in a Unit
This puzzle is quite simple up to the Rule 2 example which is the main bottleneck. Mapping all the chain links for number 7 we find something interesting in row B and column 6. There are two yellow 7s in B3 and B5. This Rule says that if any unit has the same colour twice ALL those candidates which share that colour must be OFF. The rule is also present in column6. The alternative colour will be ON and the solution for that cell.
(Actually yellow is the colour I use to show eliminated candidates. The solver will return Green and Blue for the colouring but then switch one or other to yellow if the candidates are to be eliminated). [Example updated June 2025]
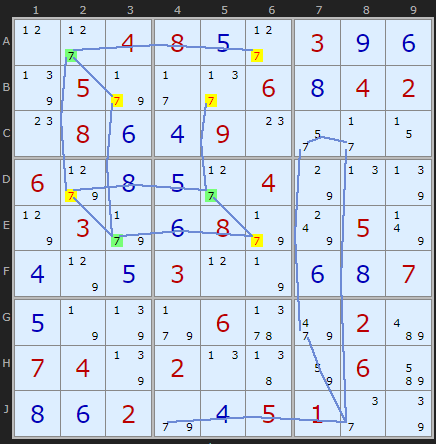
Rule 4 - Two colours 'elsewhere'
If you have looked at X-Cycles you'll spot how these two strategies overlap - if your colouring happens to form a loop, as it does here. Also, if you've read as far as AICs you may recognize the pattern of 3s as a classic double alternating Nice Loop with a discontinuity in B5. But that's another story.
Michael Wallis is an early pioneer of Simple Coloring and this rule family.
This rule is shared with 3D Medusa.
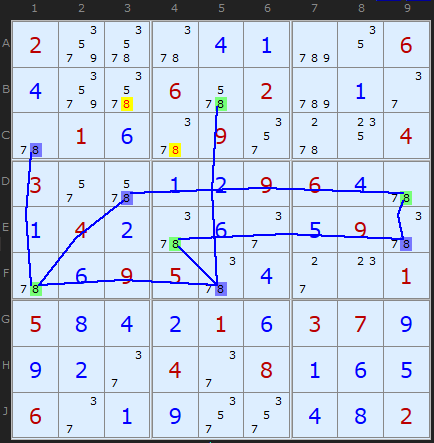
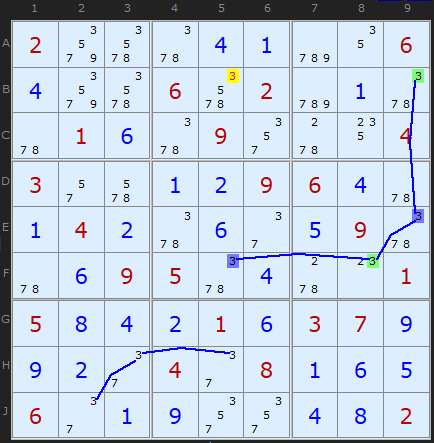
Rule 4 is simply put: if you can spot a candidate X that can see an X of both colours - then it must be removed. The third instance of this strategy concerns 8s and we can see a more complicated network of 8s than the 3s above. However, it is easy to pick out the blue and green 8s that point to the eliminations.
The documentation on this page has changed in February 2015 when a reader called FallsOffRocks wrote to me to point out the algorithm for the old Rule 5 could always get all Rule 4 eliminations. So have rolled Rule 5 into Rule 4. Both rules are examples of off-chain eliminations looking at candidates in different cells. The simplification also affects 3D Medusa.
The strategy which naturally follows on from Singles Chains is 3D Medusa, but you should also read up on the article Introducing Chains and Links.
Simple Colouring Exemplars
These puzzles require Simple Colouring strategy at some point but are otherwise trivial.All contain only one Naked Pair in addition to Simple Colouring. New examples added June 2025.
They make good practice puzzles.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: A.A.B.
... by: bern
... by: Pieter, Newtown, Oz
... by: Roman Malyniak
- the drawn 5-bi-locations links D3-E1 and D3-G3 are not valid.
- the 5-bi-locatin link G3-G7 is missing. Also this strong
link forms an ER example with boxes4 and 6,removing 5
from E3 and E7 and making the D3-E1 and D3-G3 links valid.
... by: peter
... by: Bill Howard
A better description is very necessary.
... by: jO
"Another way of looking at this...." Please what is the first way of looking at this? I am looking for a different explanation since this one is not clear.
... by: Stephen P. Byers
A similiar problem exists in your example titled "Coloring Example 1" at the end of the article. There are three 9's in Colimn 1 so how can two of them be included in the chain? Please explain.