Sue-De-Coq
This exotic strategy is strongly related to trivial patterns like Naked Pairs and Naked Triples since we are identifying Locked Sets. The building blocks are Almost Locked Sets but the most interesting aspect is the alignment of these parts.
To re-cap the terns:
To re-cap the terns:
- A Locked Set is a group of N cells that can see each other which have N candidates - an example being a Naked Pair
- An Almost Locked Set is a group of N cells which are mutually visible and share N+1 candidates in some combination.
- An Almost Almost Locked Set is a group of N cells which are mutually visible and share N+2 candidates in some combination.
- An Almost Almost Almost Locked Set is a group of N cells which are mutually visible and share N+3 candidates in some combination.
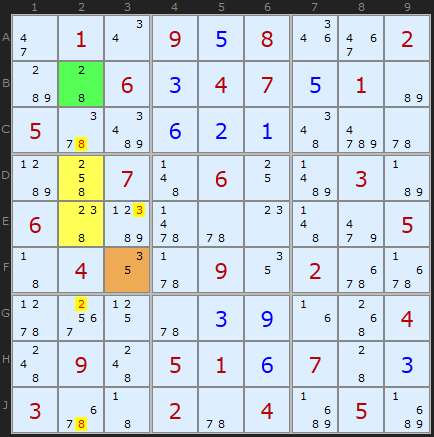
In the first example the two yellow cells (N=2) contain {2,3,5,8} which is N+2, or four candidates. The group is contained within box 4. We don't know which of the values {2,3,5,8} will be the solution to D2 and E2 but clearly two of those four will be. Now, if we look along the unit of alignment (column 2) and within the box we can find single cells that contain two of those candidates. B2 contains {2,8} (the green cell) and F3 contains {3,5}. The AALS can see these cells - which is important!
We now know that the solution to the AALS {D2,E2} cannot be 2/8 or 3/5 since it would leave nothing in the cells B2 and F3.
The logic is as follows. If neither {2/8} can fill the AALS nor {3,5} then some other combination must fill it that leaves a digit free for the single bi-value cells. So effectively {2,3,5,8} must fill all coloured cells. Indeed the group in total contains four cells and there are four candidates, so we have identified the total group as a Locked Set. This means we can remove all candidates X that see all X in the total group. This excludes the 8 in C2 and J2 (aligned in the column) and 2 G2 (also aligned in the columns) and the 3 in E3 (shares the box).
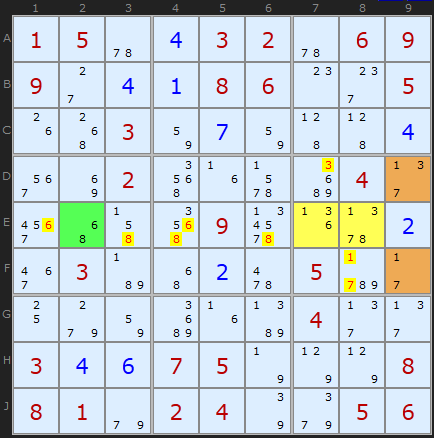
In the second example we combine an AAALS (N+3) in {E7,E8} containing {1,3,6,7,8} with two normal ALSs {D9,F9} and {E2} containing {1,3,7} and {6/8} respectively. The trick is that the total number of cells, 5, equals the total number of candidates in all the cells {1,3,6,7,8}. We get a 5-cell Locked Set.
To eliminate we look at what candidates OUTSIDE the pattern can see ALL the candidates INSIDE the pattern. These are the 6s and 8s in row E, and the 1s, 3s and 7s in box 6.
Generally then...
The general terms the rule for the pattern is as follows:
- Find a 2-cell or 3-cell group inside a box that is also aligned on a row or column - call it group C
- C contains a set of candidates, V, which must be two or more than the number of cells in C (N+2, N+3 ALS etc).
- We need to find at least one bi-value cell (or larger ALS) in the row or column which only contains candidates from set V, called D
- We need to find at least one bi-value cell (or larger ALS) in the box which only contains candidates from set V, called E
- The candidates in D and E must be different.
- Remove any candidates common to C+D not in the cells covered by C or D in the row or column
- Remove any candidates common to C+E not in the cells covered by C or E in the box


Comments