Unit Forcing Chains
If this is your first visit to these strategies, do read the article on Digit Forcing Chains which begins the explanation of this type of strategy and continues to with Cell Forcing Chains. Digit and Cell Forcing Chains are simpler to identify.
If we are forcing a result from a single cell we are obliged to look at all the numbers in that cell. But the logic can be flipped on its head by considering all of X on a unit. If you have three 8s on a row, you know one of those will be the solution. It may be possible to force an elimination by finding a target which can't be true no matter which of those 8s will it turns out to be.
I do know of some Dual Unit Forcing Chains but they are part of such nightmarish puzzles I don't want to use them for examples. They are pretty rare considering that Alternating Inference Chains are sought after first. So we are going to plunge straight into a Triple.
If we are forcing a result from a single cell we are obliged to look at all the numbers in that cell. But the logic can be flipped on its head by considering all of X on a unit. If you have three 8s on a row, you know one of those will be the solution. It may be possible to force an elimination by finding a target which can't be true no matter which of those 8s will it turns out to be.
I do know of some Dual Unit Forcing Chains but they are part of such nightmarish puzzles I don't want to use them for examples. They are pretty rare considering that Alternating Inference Chains are sought after first. So we are going to plunge straight into a Triple.
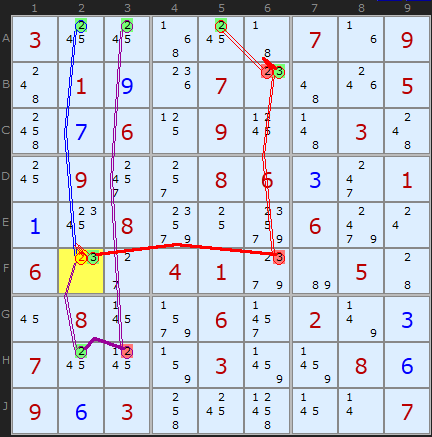
The example to the right is not too entangled. We have three 2s in row 1 on A2, A3 and A5. If any of these is the solution (and one has to be) we can show that F2 cannot be a 2. The 2 in A2 does this fine for the first chain.
The second chain, purple, from A3 means no 2 in H3 which forces a 2 in H2. Therefore 2 in F2 is knocked off. It's a short chain: +2[A3]-2[H3]+2[H2]-2[F2].
The final chain, in red, obliges B6 to be a 3 removing 3 as an option in F6. The only other 3 in row F is on F2. This chain can be expressed as +2[A5]-2[B6]+3[B6]
-3[F6]+3[F2]-2[F2]
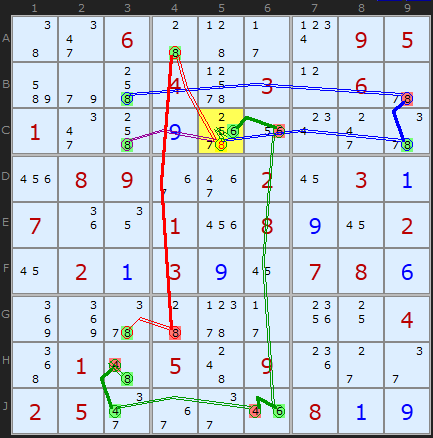
I don't pretend for a minute this is a human friendly solution to a puzzle but it is fascinating to find an example. This is a rare Quad Unit Forcing Chain, based on all the 8s in column 3. It removes the 8 in C5.


Comments