I have used (Bi-Value Universal Grave) BUG as a simple and effective technique to end a Sudoku board rapidly for quite a long time. By accident I coded a board which had two apparent BUGs, in different units, of course. In this case the BUG character that resulted was the same for both cells and I wondered whether I could validly treat these two cells as a pincer and make an elimination. This worked and after a large number of attempts in other games I have concluded that this is valid. Further I decided to try chaining from one or other pincer (as usually they were not each the same value) until I had a pincer pair that could eliminate. And from time time I found THREE apparent BUGs and the same deletions were possible, though with three “candidates”, this could be trickier.

Only recently I looked again at the description entry for BUG in Andrew Stuart’s excellent Solver. This has a standard description of BUG with some examples – but links to a blog which goes a bit further. Here I discover that BUG forms BUG+1, BUG+2 and BUG+3 have been worked on and can resolve the board, though using chaining and forcing techniques. BUG+n is used as a term and I supposed a BUG could be found in theory for all nine occurences of a unit – row, column or box. But the key point I took away is that ONE of the identified BUG characters will be correct. So I have treated these as BUG Candidates (BC)
I have developed a second difference in that I learnt long ago (from Henk Westhuis’ excellent Into Sudoku site and solver) that states one should pick the candidate with three occurrences in the unit (this in reference to a standard BUG+1). I have extended this: to be the Most Commonly Occurring Candidate so the BC can be identified as the one which occurs most often in the unit. I can find no proof of this, but this approach clearly works and is much simpler than considering Deadly Patterns. Though I realise that this is taking the technique away from its origins! I had also assumed that BCs could be found in rows, columns, or boxes, but now dissent from this as far as the techniques I describe below are concerned. I do not know why, but equally I do not really understand why the technique I describe works at all!

There is also an important condition that the board is clean, with no deletions un-done. Probably this means a clean board as in Andrew Stuart’s excellent solver after the first six steps, and I have adopted this in the examples that follow.

Of course, as currently understood, the technique may be interesting, but it resolves only quite simple situations, and those at the end of the solution of a game.

However, I appear to have progressed the technique somewhat – and this by utilising two things:
(a) That BCs can be manipulated like any other pincer value; and
(b) by identifying BCs using my “most commonly occurring” principle. I refer to BCs occurring in boxes only.

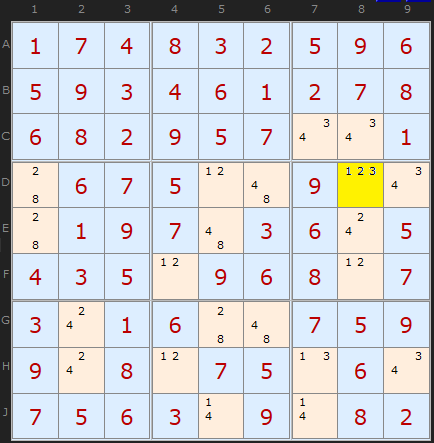
The simple BC is to the right – the first example in Stuart’s description:

He identifies the BC as “2” in D8. And according to my technique the most commonly occurring candidate value in the box is also 2 and it relates to the cell with the most values (in this case three – 1 2 3). In the examples in the PDF it is simpler to show just a single box and ignore the rest of the board for the purpose of explanation.

Now, identifying BCs as I have done thus gives rise to some other permutations, and involving more unresolved candidates on a board.

The rest of the discussion and examples continues in the PDF document below.

Link to PDF document (1.7Mb)