A Set Theory Approach to Sudoku Strategies
Abstract: 'Generalizing Sudoku Strategies'

This paper seeks to define a smaller set of more generalized strategies, which make the relationship among some of the named strategies more explicit, suggest other strategies for solving puzzles, and offer a path to simplify Sudoku solvers.
Using set notation, this paper defines six generalized strategies which encompass sixteen or more individual strategies. These generalized strategies may be implemented in computerized algorithms.
The paper concludes with some thoughts on ranking puzzle difficulty, and on open questions involving the completeness and efficiency of Sudoku solution strategies.
by Kevin Gromley, March 2014
This is a fascinating paper by Kevin Gromley who has set out a way to group families of logical strategies based on 'constraint sets'. I'm not nearly mathematical enough to appreciate the set theory formulas but we have exchanged ideas about the conclusions of this paper and discussed some of the open questions. I'd like to pick out a few points and write about them here.
- Firstly, it's worth re-iterating what a 'logical' Sudoku strategy really *is*. The strategies on this site are dominated by what I called 'pattern' based logic - that there is a pattern in the candidates on the board and we can make a deduction about some of the numbers that leads to candidates being removed and cells solved. Kevin has coined the excellent term State Deterministic to say the same thing and I'm completely won over by this term. From the initial puzzle the state of the board as it exists determines the next state - and through a series of steps we take the puzzle through to the solution.
I contrast this with strategies that require you to change the board and see what happens. So called 'trial and error strategies' like "if that cell was a 3, does it work out or not". These can be applied in a logical and rational way so in a weak sense it is 'logical' but most solvers would agree that it is akin to guessing and much less elegant. - Before my discussion with Kevin I was of the belief that for logical strategies to work on a puzzle the puzzle has to have a unique solution. This is true but there is in fact a stronger relationship between uniqueness and logic. Because State Deterministic strategies are subtractive in nature a puzzle solved in this way means that we have *proved* the puzzle has a unique solution. This is an important point because a guessing strategy can never prove a single solution unless it exhaustively tests every value in every cell. The brute-force 'Solution Count' does this in extremis.
So if we cannot solve a puzzle using State Deterministic strategies either the puzzle is faulty or we don't have enough strategies. Kevin's work has set out proofs using constraint sets that envelope a large number of strategies proposed on this site. That is impressive but some puzzle solutions are still out of reach using only those tools. Nevertheless, it holds out hope that we can solve all puzzles using these methods. I see many complex and interesting solutions on the Weekly Unsolveables Puzzles that show a state deterministic solution on an individual basis.
- Another point the paper discussed was the efficiency of the strategies. For a given Sudoku puzzle, is there an a priori way to determine or estimate an efficient set of rules to apply? On one hand this is a very practical question since I am very interested in optimizing solving algorithms. It takes time to test a large set of difficult puzzles. But this question is bound up with the notion that there are many paths to solving a puzzle even though there is only one start position (the puzzle) and one end position (the solution). It may not matter to the pen and paper solver whether their solution is the best solution - but does State Determinism tell us anything about the *best* and *shortest* solve path? Without exhaustively testing all paths?
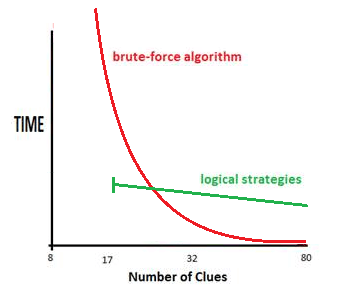
I knocked up a quick graph to show the very rough relationship between logical strategies and brute-force - the two competing approaches to finding solutions. Brute Force is incredibly fast at high numbers of clues. I've dropped in 17 as the minimum number of clues on a normal Sudoku - my implementation can take a few seconds on these puzzles. The 8 is the smallest number of clues in a Jigsaw Sudoku - expotentialism takes over and I've never waited long enough to see how long it takes.
The straight green line should be a rather hazy line because clue density has almost no bearing on the complexity of the puzzle except in the gross sense of less or more availability for steps. There are trivial 17 clue puzzles and horrendous 30 clue ones. But logical strategies only take 5-10 seconds on the hardest puzzles and so the time spread is fairly flat.
- Andrew Stuart

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.