Bowman's Bingo
This is the last of the "last resort" strategies, often derided as Trial and Error. Bowman’s Bingo suffers from the problem of choosing a starting cell as we’ll see, but its one of the few bifurcating strategies that works well for a human, if you’ve got the equipment. MadOverLord came up with the idea and named it after Doug Bowman for his work on Colouring. The Bingo comes from the translucent Bingo chips that work best as place markers. You can do this with bits of paper on a large grid as well as chips - but all must be marked with the numbers 1 to 9 and the sides must be distinguished between up and down. Your grid should have all the candidates marked - the point where you’ve become stuck.
We’re going to test for a contradiction that allows us to eliminate a candidate. Choose a cell you want to test and a number in that cell that’s a possible candidate. Place a chip with that number on the cell face down. To "flip" a chip is to turn it over.
Now the following steps should be repeated:
We’re going to test for a contradiction that allows us to eliminate a candidate. Choose a cell you want to test and a number in that cell that’s a possible candidate. Place a chip with that number on the cell face down. To "flip" a chip is to turn it over.
Now the following steps should be repeated:
- Choose any face down chip and turn it face up. (if you’ve just started then it’s the chip you just placed).
- All candidates that this chip number can see must be marked with an face down chip. Look along the rows, columns and in the box for this candidate and place face down chips on those cells if they have this number.
- Face down chips represent values that are suppressed - that is they are not solutions in the current state of the strategy. Where you placed new chips you might find cells that are forced to be single values. A bi-value cell with 1/9 for example - if it has an face down chip of ‘9’ is now a single value of 1. Place an Up facing chip on these.
- Check for a contradiction. Any row, column or box with two chips of the same number that are both either face up or face down mean a contradiction. If you find such a configuration then the original candidate you were testing can be removed.
- If you have any face down chips go back to step 1
If you end up with all your chips face up and no contradiction then you’re not a winner. Clear the chips and try another cell and candidate. If you’ve managed to cover ALL the unsolved squares with face-up chips then you’ve lucked into the solution. Say "Bingo" out loud!
Bowman’s Bingo doesn’t solve all ‘bifurcating’ Sudokus but if applied thoroughly it will crack more than 80% of them. It’s not a panacea like Tabling or Nishio but it is easier to do and will work better if you are down to your last twenty or so unsolved squares.
As a logical process this follows on from many of the chaining techniques discussed earlier. However, when chains branch they are called ‘nets’ and Forcing Nets are closest to this strategy.
All candidates on the board have one of four states. They are either Untested, Killed, Up or Down. Chips on the board make a candidate either Up or Down. When you flip a chip to turn it up you are saying “that’s the solution" for that cell. This "Kills" all the other candidates in that cell and you should mentally clear any other down chips on that cell. This is important since we don’t want two up-chips (two solutions) on the same cell.
Here’s an Evil Sudoku which can now be solved with other strategies but I retain it as the example because re-doing images and example is too much work :)
Bowman’s Bingo doesn’t solve all ‘bifurcating’ Sudokus but if applied thoroughly it will crack more than 80% of them. It’s not a panacea like Tabling or Nishio but it is easier to do and will work better if you are down to your last twenty or so unsolved squares.
As a logical process this follows on from many of the chaining techniques discussed earlier. However, when chains branch they are called ‘nets’ and Forcing Nets are closest to this strategy.
All candidates on the board have one of four states. They are either Untested, Killed, Up or Down. Chips on the board make a candidate either Up or Down. When you flip a chip to turn it up you are saying “that’s the solution" for that cell. This "Kills" all the other candidates in that cell and you should mentally clear any other down chips on that cell. This is important since we don’t want two up-chips (two solutions) on the same cell.
Here’s an Evil Sudoku which can now be solved with other strategies but I retain it as the example because re-doing images and example is too much work :)
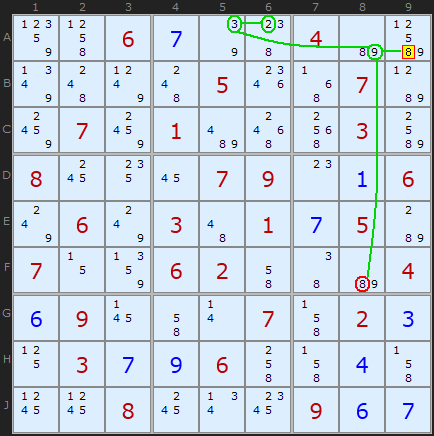
This example starts on A9, candidate 8. We put the 8 clip face up saying in effect, we believe 8 to be the solution to this cell. This puts face down chips on A8(8) which since it is a bi-value cells gives us 9 on that cell. Looking along the row A, 3 also falls into place on A5 giving us 2 on A6. Down the column we can flip the 9 down on F8 and this gives us 8 on that cell.
In previous articles I have used ON and OFF to give the same effect and you can think in terms of this as well. The difference between Bowmans and previous chaining is that we are clearing off the candidates en mass when a chip is turned up.
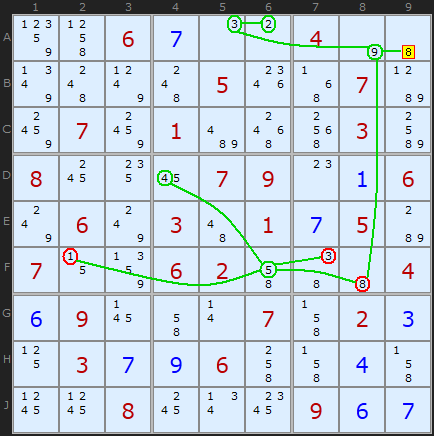
So from F8 we flip chips along the row giving us solutions for F6 (5), then F2(1) and D4(4).
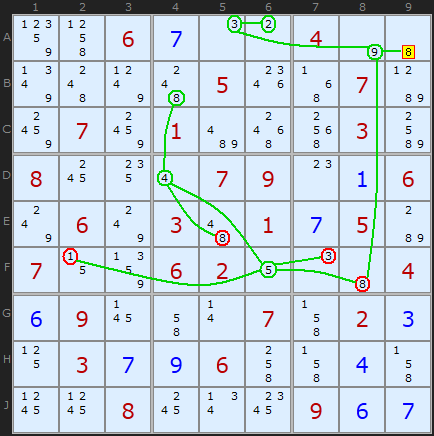
Continuing from wherever we got to we flip and turn on the 8s in B4 and E5
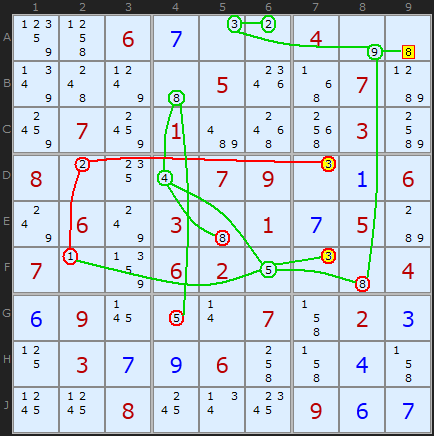
..until finally we hit a contradiction. The 2 in D2 derived from the 1 in F2 means we can place a 3 in D7.
But! There are now two 3s in column 7 - a contradiction. The solver will return the message:
BOWMAN BINGO: A9 cannot be 8 because the last remaining candidates in cells D7 and F7 are both 3
So 8 can be removed from A9.
The solver will display a whole set of red and green candidates. This is the result of all the branches and chip flips it has done up to the elimination. It's not very clear and in a future version I hope to improve the display.
Personally I think the method as originally described is a little over methodological, since we have just drawn a forcing net. But for me it crosses the line into 'trial and error' because it is so arbitrary - both the initially selected cell and the branching off in every direction. It is a true bi-furcation method. But it is presented here as one method of searching for eliminations when all else fails.
Personally I think the method as originally described is a little over methodological, since we have just drawn a forcing net. But for me it crosses the line into 'trial and error' because it is so arbitrary - both the initially selected cell and the branching off in every direction. It is a true bi-furcation method. But it is presented here as one method of searching for eliminations when all else fails.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: gstefanidakis@gmail.com
... by: Ed
I'm doing a puzzle right now and at one point the only strategy that the solver uses to find something is the Bowman's Bingo. Unfortunately, the solver doesn't give the details of how it came to this conclusion. I think it would be a great addition to the programming to give the details.
Here is the import code for the puzzle from the beginning
Here is the import code for the puzzle when it's at the point of requiring the Bowman's Bingo strategy:
... by: ATechGuy
You could also keep the green drawing going to show this value being taken in A2.