BUG
BUG stands for Bi-Value Universal Grave
The principle behind BUG is the observation that any Sudoku where all remaining cells contain just two candidates is fatally flawed. There would have been a last remaining cell with three candidates. The odd number that couldn't be paired with another cell would have to be the solution for that cell in order to prevent the bi-value 'Graveyard'.
Thanks to Peter Hopkins for re-engaging me with BUG (July 2015). He has found the original discussion which goes back to November 2005. Here is the link. From my testing of large data sets I believe that every instance of BUG can be solved by an XY-Chain. Hence it is positioned just before that strategy in the solver - it is an easy solution if you can recognise the pattern. Other simpler strategies may also do the same job but not as completely as XY-Chains.
The principle behind BUG is the observation that any Sudoku where all remaining cells contain just two candidates is fatally flawed. There would have been a last remaining cell with three candidates. The odd number that couldn't be paired with another cell would have to be the solution for that cell in order to prevent the bi-value 'Graveyard'.
Thanks to Peter Hopkins for re-engaging me with BUG (July 2015). He has found the original discussion which goes back to November 2005. Here is the link. From my testing of large data sets I believe that every instance of BUG can be solved by an XY-Chain. Hence it is positioned just before that strategy in the solver - it is an easy solution if you can recognise the pattern. Other simpler strategies may also do the same job but not as completely as XY-Chains.
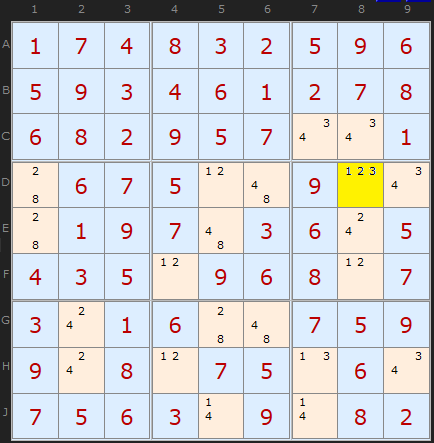
The BUG cell is D8.
Removing candidate 1 from the cell does not create a deadly pattern, since candidate 1 would appear in Row D, Column 8 and Box 6 just once. Removing candidate 2 results in:
- Row D containing candidates 1, 2, 3, 4 and 8 all exactly twice.
- Column 8 containing candidates 1, 2, 3 and 4 all exactly twice.
- Box 6 containing candidates 1, 2, 3 and 4 all exactly twice.
- Every other unit containing unsolved cells in which all candidates appear exactly twice.
Thus, in order to kill the BUG, D8 must be 2.
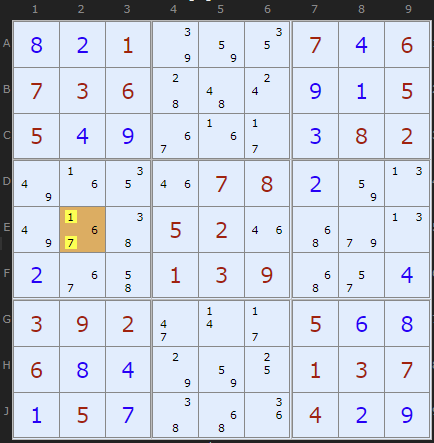
It is possible for the BUG to exist in a sea of bi-value cells, such as this one discovered by Klaus Brenner. It is also notable for have two whole boxes with only bi-value cells.
BUG Exemplars
These puzzles require the Bi-Value Universal Grave strategy at some point.Only the first is somewhat trivial. They make good practice puzzles.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.