Hidden Candidates
Hidden Pairs
Looking for Hidden Pairs is a great way to open up the board. This approach can remove a cluster of candidates from two cells and leave behind simple pairs which are the building blocks of more complex elimination strategies.
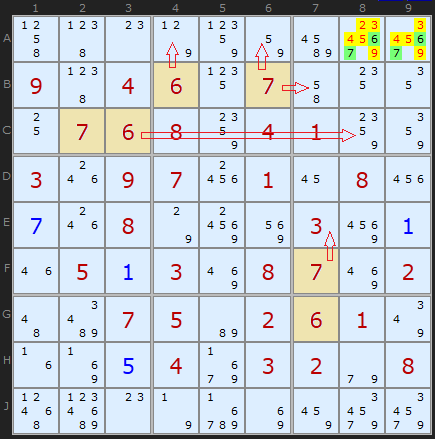
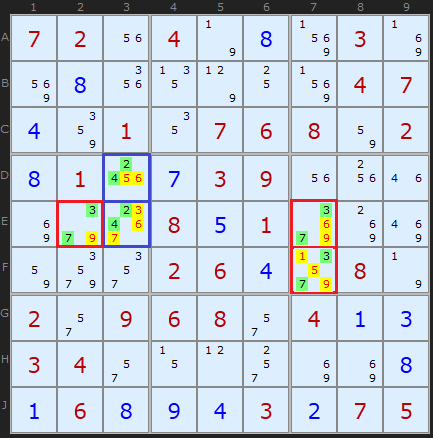
This is a more interesting and complex set of Hidden Pairs. Three occur simultaneously. In the blue rectangle, [2,4] form a Pair on D3 and E3, clearing off 3, 5, 6 and 7. The red cells indicate two Hidden Pairs based on [3,7], which form a neat corner of three cells. [3,7] is unique to two cells in row E and two cells in column 7. The yellow highlighted cells can be removed.
Hidden Triples
We can extend Hidden Pairs to Hidden Triples or even Hidden Quads. A Triple will consist of three pairs of numbers lying in three cells in the same row, column or box, such as [4,8,9], [4,8,9] and [4,8,9]. However, in just the same manner as Naked Triples, we don't need exactly three pairs of numbers in three cells for the rules to apply. Only that in total there are three numbers remaining in three cells, so [4,8], [4,9] and [8,9] is equally valid. Hidden Triples will be disguised by other candidates on those cells, so we have to prise them out by ensuring the Triple applies to at least one unit.
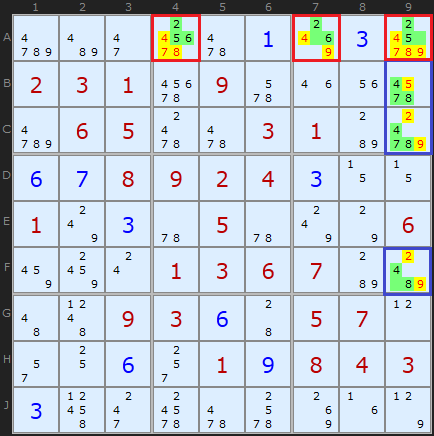
This tough puzzle has two Hidden Triples: the first, marked in red, is in row A. Cell A4 contains [2,5,6], A7 has [2,6] and cell A9 contains [2,5]. These three cells are the last remaining cells in row A which can contain 2, 5 and 6, so those numbers must go in those cells. Therefore we can remove the other candidates.
Now that we've removed those candidates from the red cells, we can see in column 9 that [4,7,8] is unique to cells B9, C9 and F9. By the same logic we can clear off other candidates in those cells.
(The solver will not choose the second example as Naked Triples get there first)
Hidden Quads
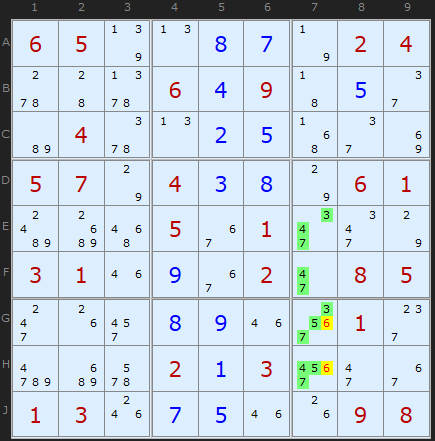
Here is the one example of a Hidden Quad I found in a set of 18,000 Sudoku puzzles. Four numbers [3/4/5/7] on four cells are hidden by just two 6s in column 7. Barely qualifies as 'hidden', but it is legitimate. Note how none of the cells need to have all four numbers, as long as only four cells contain all four numbers and are intermingled.
Hidden Quads almost always only occur in rows, columns and boxes where there are no clues or solved cells, so you can be forgiven for skipping them outside those circumstances.
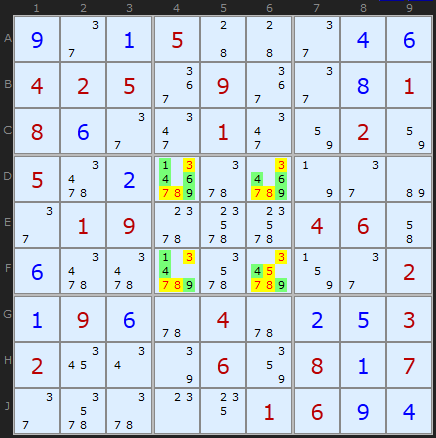
Klaus Brenner in Germany has found a number of excellent Hidden Quads, and I include one here to show they do exist.
The Hidden Quad is {1,4,6,9} in Box 5 and exists only in the four cells [D4,D6,F4,F6]. Therefore other candidates (red text on yellow background) can be removed.
This very special puzzle also produces a perfectly formed Empty Rectangle later on.
We don't consider higher orders of Hidden candidates because there are only 9 cells in a unit. So if we were to suppose a "Hidden Quin" with five candidates there would automatically be a complementary Hidden Quad since 5 + 4 = 9. Same point arises with Naked sets. It may be viable to look for such beasts in 12x12 or 16x16 Sudokus.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: marten van der meer
... by: marten van der meer