Unique Rectangles
Unique Rectangles takes advantage of the fact that published Sudokus have only one solution. If your Sudoku source does not guarantee this then this strategy will not work. But it is very powerful and there are quite a few interesting variants.
Credits first: The initial ideas for these strategies I lifted wholesale from MadOverLord's description (11 Jun 05) on the forum at www.sudoku.com. (Sadly the thread is no longer hosted). Many others have since added to and improved them. I have provided my own examples. (please email me for other credit requests). I will stick to MadOverLord's nomenclature.
Credits first: The initial ideas for these strategies I lifted wholesale from MadOverLord's description (11 Jun 05) on the forum at www.sudoku.com. (Sadly the thread is no longer hosted). Many others have since added to and improved them. I have provided my own examples. (please email me for other credit requests). I will stick to MadOverLord's nomenclature.
 27th January 2025
27th January 2025
Added the ability to cycle through all Unique Rectangles found when the first is displayed.
Similar to how chains can cycle.
Noticing the 'Deadly Pattern'
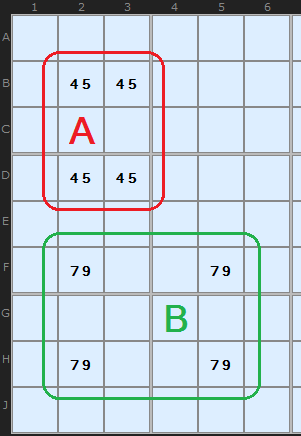
The pattern ringed in green looks like a deadly pattern but there is a crucial difference. The 7/9 still resides on two rows and two columns, but instead of two boxes it is spread over four boxes. Now, such a situation is fine since you can't guarantee that swapping the 7 and 9 in an alternate manner will produce two valid Sudokus. One of them is the real solution, the other a mess. Why? Swapping the 7 and 9 around places them in different boxes and 1 to 9 must exist in each box only once. In the red example, swapping within the box does not change the content of that box.
Type 1 Unique Rectangles
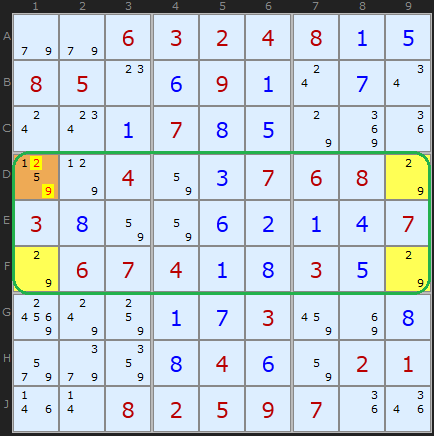
The proof is pretty straightforward once you get your head around the basic idea. Assume D1 is 2. That forces D9 to be 9, F9 to be 2, and F1 to be 9. That's the deadly pattern; you can swap the 2's and 9's and the puzzle still can be filled in. So if the Sudoku is valid, D1 cannot be 2. The exact same logic applies if you assume D1 is 9.
So D1 can't be a 2, and can't be a 9
- it must be either 1 or 5.
Type 2 Unique Rectangles
In Figure 3 we have a similar pattern, but this time, A5 and A6 (cells which are also in the same box) both have a single extra possibility - in this case, 7.
To make subsequent discussion easier to follow, we will refer to the two squares that only have two possibilities as the floor squares (because they form the foundation of the Unique Rectangle); the other two squares, with extra possibilities shall be called the roof squares.
To make subsequent discussion easier to follow, we will refer to the two squares that only have two possibilities as the floor squares (because they form the foundation of the Unique Rectangle); the other two squares, with extra possibilities shall be called the roof squares.
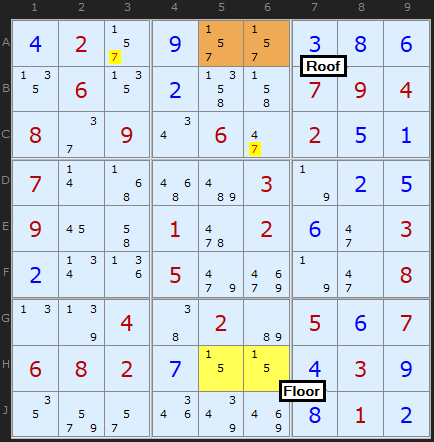
Now that you've gotten your head around the basic unique rectangle concept, the proof should come clear:
If neither A5 or A6 contains an 7, then they both become cells with possibilities 1/5. This results in the deadly pattern - so one of those cells must be the 7, and none of the other squares in the intersecting units can contain 7. So A3 and C6 can have 7 removed. This cracks the Sudoku.
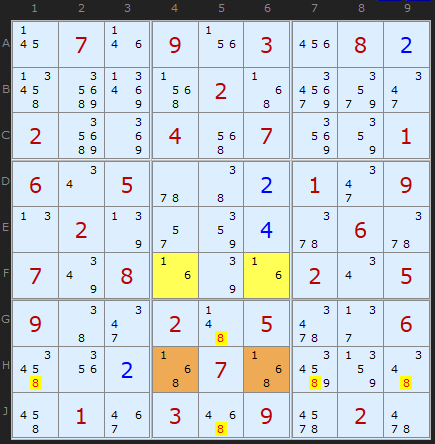
I couldn't resist adding this example which I found while looking for Empty Rectangles. It's as clear as day how the 8s in H4 and H6 combine with the [1,6] Deadly Pattern. 8's aligned with the brown cells are eliminated. I need say no more.
To view this puzzle in the solver uncheck Rectangle Elimination and choose the second Unique Rectangle after the Type 5 which is found first.
Type 2B Unique Rectangles
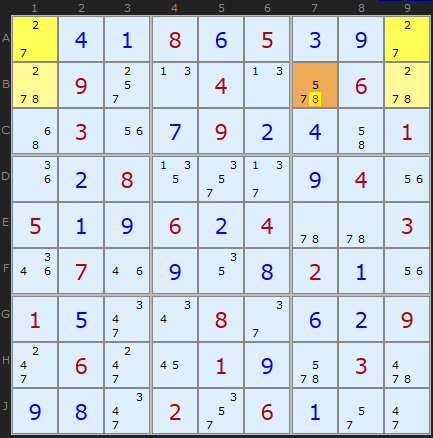
In this puzzle, we have the same pattern of 4 squares in 2 boxes, 2 rows and 2 columns. The floor squares are A1 and A9, and the roof squares are B1 and B9. However, in this Unique Rectangle, each of the boxes contains one floor and one roof cell. This is perfectly fine, but it means that the only unit (row/column/box) that contains both of the roof cells is row 2, so that is the only unit that you can attempt to reduce; in this case, B7 cannot contain a 8. This is called at "Type-2B Unique Rectangle".
You will need to untick 3D-Medusa to see this example.
Type 2C Unique Rectangles
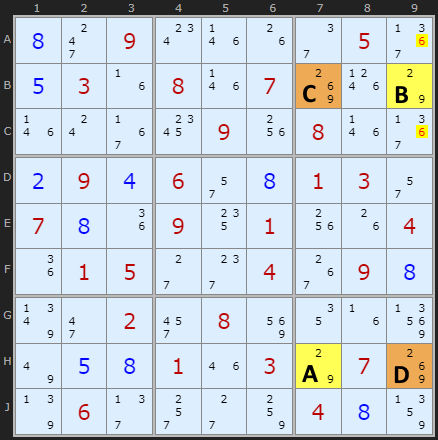
This variation again has the extra candidate but in cells diagonally opposite. You can see the extra 6 in cells B7 and H9 (marked as C and D). 6 Must exist in one of those two cells so any 6 not in the deadly rectangle pattern that can 'see' C and D can be removed.
Not shown in the example is the chance that A or B can also contain the extra candidate 6. Lets say B did - the eliminations hold since those cells can see B9. But if the third extra candidate was in H7 then we could not look in box 3.
Type 3 Unique Rectangles
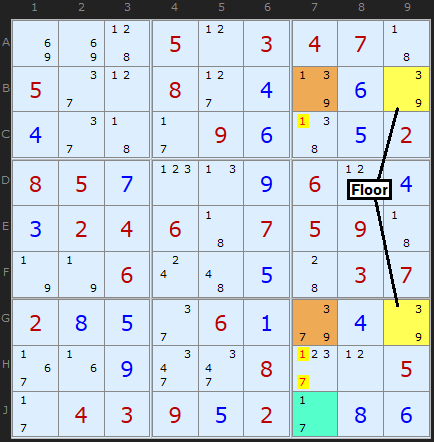
In this variant we have a floor with a pair as before but the roof contains two different candidates (occurring once or twice in each cell of the roof). In the Figure 7 the floor and roof contain [3/9] and the extra candidates in the roof are 1 and 7. Removing both the 1 and 7 from the roof would leave the deadly pattern so either the 1 in B7 must be a solution or the 7 in G7 is a solution. Knowing this does not get us as far as an elimination, however, but we can say that the 1 in B7 and the 7 in G7 act as a pseudo-cell in their own right. The clever bit is using this pseudo-cell with a bi-value cell containing the same candidates. Such a cell is circled on the board – J7. We effectively have a “locked set” like a Naked Pair. 1 will occur in B7 or J7 or 7 will occur in G7 or J7, we just don’t know which way round.
Such reasoning allows us to remove other 1s and 7s on the unit shared by the roof cells (but not the cell we’re using to create a locked set with). There are 1s and 7s in C7 and H7 which can be eliminated.
Type 3b Unique Rectangles
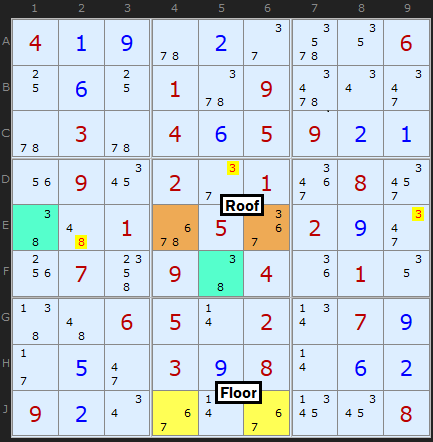
There is a compliment to Type 3, where the roof cells share the same box and that means the floor must be in a different box. Cells J4 and J6 form a pair with 6 and 7. These can see two cells in row E which also contain 6/7 as well as a 3 and an 8. We need to match this 3 and 8 in the roof cells with a bi-value cell to make a locked set (effectively a Hidden Pair). As we have roof cells in the same row AND box we can look in both row 5 to E1 and remove all other 3s and 8s in the row, plus F5 and eliminate 3 from D5.
I'd like to credit Hervé Gérard for the first example which he sent to me in November 2013 and later Tom Morrin for stating the box should be used as well.
Type 3/3b with Triple Pseudo-Cells
So far Type 3 and 3b have worked with a pseudo-cell linking with a bi-value cell to make a pseudo pair. This is a valid locked set. Well, locked sets don't have to be pairs, they can involve three candidates over three cells.
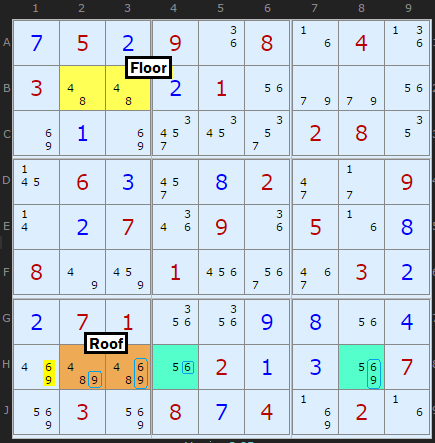
All credit to David Hollenberg for working this insight that nicely expands the strategy. In a test of 5,000 puzzles with some kind of UR, a third more Type 3 and 3B were found with Triples. (Update: Alas due to the search order a Type 5 is discovered first).

(untick XY-Chains) : Load Example or : From the Start
Here is a triple with a slightly different pattern, also from David Hollenberg.
There are three candidates {1, 4, 6} in the pseudo-cell (the extra candidates in the roof). Instead of looking for an extra candidate to make up triple in two other cells we look for all three candidates {1, 4, 6} in two other cells. These are in A9 and C9. These form a triple with the pseudo-cell in GJ9. Naked Triple rules apply so we can eliminate the 4 in E9 and the 4 in H9.
Uniqueness Type 3b (Col) at GJ49
- removing 4 at E9 (triple with A9+C9)
- removing 4 at H9 (triple with A9+C9)
Type 4 Unique Rectangles
- Cracking the Rectangle with Conjugate Pairs. (See also Extended UR Type 4.)
An interesting observation is that it is sometimes possible to remove one of the original pair of possibilities from the roof squares. Consider the following puzzle in Figure 10 which is a continuation of the Sudoku puzzle used in the first example.
Look closely at the roof squares, A4 and A6, but this time, don't look at their extra possibilities; look at the possibilities they share with the floor squares.
An interesting observation is that it is sometimes possible to remove one of the original pair of possibilities from the roof squares. Consider the following puzzle in Figure 10 which is a continuation of the Sudoku puzzle used in the first example.
Look closely at the roof squares, A4 and A6, but this time, don't look at their extra possibilities; look at the possibilities they share with the floor squares.
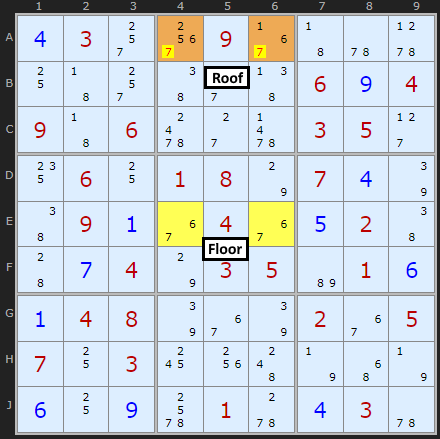
If you look carefully, you'll see that in box 2, the roof squares are the only squares that can contain a 6. This means that, no matter what, one of those squares must be 6 - and from this you can conclude that neither of the squares can contain a 7, since this would create the "deadly pattern"! So you can remove 7 from A4 and A6.
Nomenclature: When two squares are the only two squares in a unit that can have a particular value, they are referred to as a conjugate pair on that value.
This is an example of a "Type-4 Unique Rectangle". As you have probably realised, since the roof squares are in the same box, you can search for conjugate pairs in both of their common units (the row and the box, in this case).
Type 4B Unique Rectangles
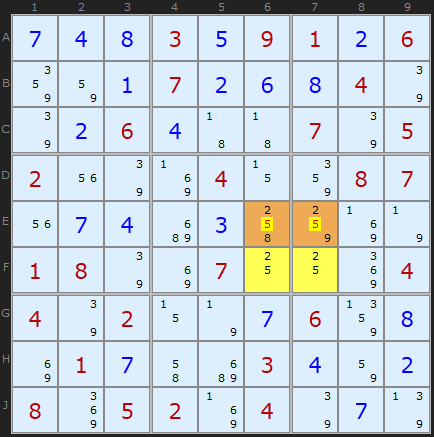
In this case, since 2 can only appear in row E in the roof squares, 5 can be removed from both of them.
As Type-4 Unique Rectangle solutions "destroy" the Unique Rectangle, it is usually best to look for them only after you've done any other possible Unique Rectangle reductions.
Type 5 Unique Rectangles
As of January 2021 we have a new Unique Rectangle elimination! Thanks to Ivar Ag�y from Norway who shared an example with me. Not to say that it might have been discovered elsewhere, I can't check, but please come forward if there are earlier references. Since it is vaguely related to Type 1 (in that it attacks candidates in the rectangle, not outside), and is quite simple to spot, the solver searches for it after Type 1 and before the others. However, I am obliged to call Type 5 since I don't want to re-number everything.
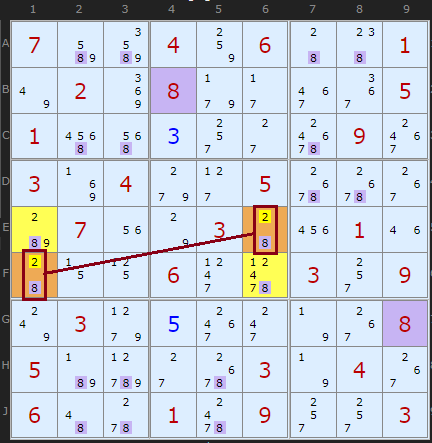
Any rectangle across two boxes that contains two candidates in all four cells might have two opposite corners containing only two candidates, like the {2,8} in E6 and F1. If one of those candidates is linked to the other corners with strong links (ie no other n in the two rows and two columns of the rectangle), it could create a Deadly Rectangle. We are looking for a diagonal Naked Pair - each cell can't see the other, but it is locked. If 2 (the weakly linked candidate in the pair) was ON in either E6 or F1 it would force 8 to be in the other corners. This is not allowed so 2 can be removed from the Naked Pair. Very cool.
Ivar's example can be found if you turn off 3D Medusa first.
(untick XY-Chains) : Load Example or : From the Start
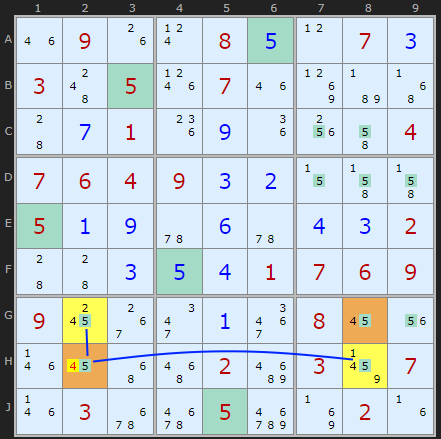
Up to 2024 I was detecting a pattern where all four candidates (8 in the example above) had strong links forming a loop all the way round. This was too restrictive. If just one pair of strong links exists we can eliminate on one end. In this example there are strong links from H2 to G2 and from H2 to H8. So if H2 is 4 then both G2 and H8 are 5, causing G8 to be 4. But this is a deadly pattern, so H2 cannot be 4.
Uniqueness Type 5: removing 4 from H2 because if true it would create a Deadly Rectangle with G2 and H2
Unique Rectangle Exemplars
These puzzles require two Unique Rectangle strategies at some point but are otherwise trivial and only requires singles.They make good practice puzzles.
Created by Klaus Brenner

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Another sudoku enthusiast
In the 2nd paragraph we are talking about eliminating the 6 but you accidentally use 9 in the explanation. It's very confusing for newbies like me.
No complaints. Just making it easier for the next person.
Thanks for the effort.
You did a great job with this wiki.
... by: Pieter, Newtown, Oz
Trying to get my head around UR's (not for the first time).
I believe that in Type 3, at the end of the paragraph "We effectively have a “locked set” like a Naked Pair. 1 will occur in G7 or J7 or 7 will occur in G7 or J7, we just don’t know which way round." should read "... 1 will occur in B7 or J7 ..."