A New Metric for Difficult Sudoku Puzzles?
This article pursues some interesting ideas being discussed on the Weekly Unsolvable Sudoku page. Fariande has posited the notion of Optimal Solutions Using Only The Basic Strategies 1-6 In the Solver, namely Singles, Pairs, Triples, Quads and Intersection Removal. I will define trivial as any puzzle that can be solved with these strategies alone. All puzzles I grade as gentle, almost all moderate and some tough ones will be of this kind.
Fariande's approach is this: should a puzzle, using the solver, require more advanced strategies to continue we stop and look at the remaining uncompleted cells. The question is, are there any cells, which if filled in with a solution, would render the remaining puzzle trivial? That is, if I know the solution of cell X, would it allow us to skip all the advanced strategies? (Fariande is not alone in thinking about this approach and on the Player's Forum these cells are called Magic Cells, which I'll use from now on.)
Fariande offers a way to identify a Magic Cell but I'm not won over that it is a practical or satisfying strategy to use for solving difficult puzzles. However, the question is interesting as we can test a difficult puzzle for the number of Magic Cells that do render a puzzle trivial. If a puzzle has twenty different cells which all lead to a trivial solution then guessing (to throw in a quick strategy) will skip a bottleneck and the puzzle ought to be considered easier than a puzzle where no cell solution will render the puzzle trivial. This allows us to distinguish two puzzles of similar grade and may be a new metric for difficulty.
Here is an example: Puzzle 1 is an extreme with a score of 1369. It apparently has 38 Magic Cells which would trvialise the puzzle. A 3 in A2 will do it. But Puzzle 2 with a score of 1347 has exactly no cells that will lead to a trivial solution. However ten percent of any two cells selected will trivialise it, for example 6 in A1 and 8 in A4. If a puzzle contains Magic Cells that individually trivialise the puzzle I call these Level-1 puzzles, while those that require two insertions I call Level-2 puzzles.
As this all started with the so called Unsolvables. I have graphed here all 114 puzzles in the system - only 61 of which have been revealed on the site so far.
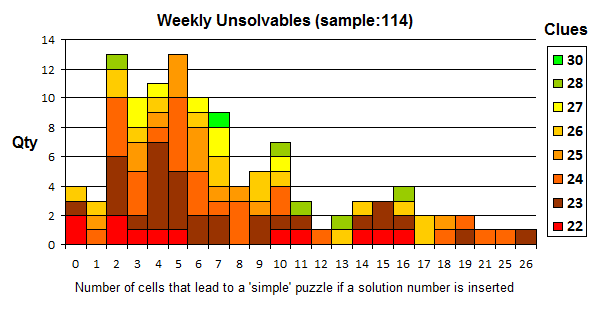

The unsolvable puzzles range in clue density from 22 to 30. I have elsewhere shown that the number of clues is not a major factor in determining the grade of a puzzle (it might prolong the experience which can cause a grade bump if the number of opportunities to solve in each 'round' is low) but I suspected that clue density would be a factor in this question, so I have coloured the graph to show it.
The sample size here is not enough to draw any conclusions but those who have solved the unsolvables are able to distinguish the easier ones from the harder ones and I believe it is related to where they sit on the chart. Unsolvable #61 has been panned as rather easy because it has 17 cells which lead to a trivial solution if these cells are known. I will be withdrawing those unsolvables > 10 that have not been published so far.
The interesting puzzles are those with zero cells that lead to trivial puzzles. These are number 4 (mine), number 29 (by Klaus Brenner) and number 28 and number 49 by David Filmer. If these puzzles do not have a single cell that leads to a trivial solution, perhaps two are required. This is indeed the case. The discussion also asked the question, are there any puzzles that require three or more cells to 'unlock'. More of that later.
Klaus Brenner has been in contact with me a good deal recently and has supplied 500 puzzles currently 'unsolvable' on my solver and I'm honoured to publish some of these. It is also a good sample set so I have worked out the chart.
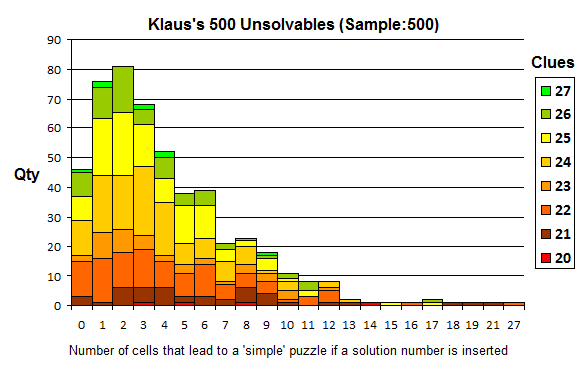
46 out of 500 puzzles are 'zero' puzzles and the chart is nicely stacked to the left which I take to indicate a greater overall difficulty than my usual unsolvables. Klaus us searching for certain kinds of patterns and has steered his approach towards unsolvables whereas I have to wait for mine to pop out of general stock production, but I can see room for improvement. His clue density is three points lower than mine overall.
The sample size here is not enough to draw any conclusions but those who have solved the unsolvables are able to distinguish the easier ones from the harder ones and I believe it is related to where they sit on the chart. Unsolvable #61 has been panned as rather easy because it has 17 cells which lead to a trivial solution if these cells are known. I will be withdrawing those unsolvables > 10 that have not been published so far.
The Zero Puzzles
The interesting puzzles are those with zero cells that lead to trivial puzzles. These are number 4 (mine), number 29 (by Klaus Brenner) and number 28 and number 49 by David Filmer. If these puzzles do not have a single cell that leads to a trivial solution, perhaps two are required. This is indeed the case. The discussion also asked the question, are there any puzzles that require three or more cells to 'unlock'. More of that later.
Klaus's set
Klaus Brenner has been in contact with me a good deal recently and has supplied 500 puzzles currently 'unsolvable' on my solver and I'm honoured to publish some of these. It is also a good sample set so I have worked out the chart.

46 out of 500 puzzles are 'zero' puzzles and the chart is nicely stacked to the left which I take to indicate a greater overall difficulty than my usual unsolvables. Klaus us searching for certain kinds of patterns and has steered his approach towards unsolvables whereas I have to wait for mine to pop out of general stock production, but I can see room for improvement. His clue density is three points lower than mine overall.
17 Clue Puzzles
So what about 17 clue puzzles? I suspected that due to the lack of clues there ought to be many more puzzles with low numbers of trivialising cells. I have a copy of the publically available set of about 46,000 17 clue puzzles and I often use them for testing. Since they are of all grades we have to discard most - any easy puzzle will be trivial from the word go. This left 7494 and I plot them in the chart here:
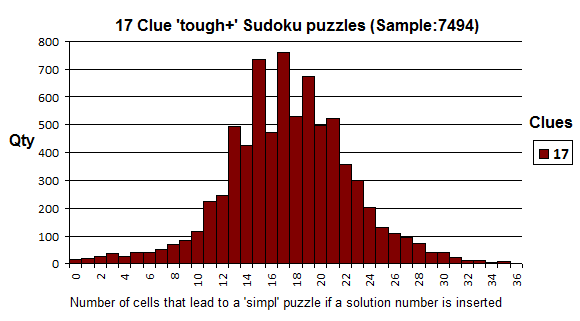
What is interesting is we get a normal or 'bell' curve. Only 16 puzzles are 'zero' puzzles with no cells leading to trivial puzzles. One of these I grade as 'tough' [Load], five are diabolical (for example [Load] and the remaining are extreme (for example [Load].

What is interesting is we get a normal or 'bell' curve. Only 16 puzzles are 'zero' puzzles with no cells leading to trivial puzzles. One of these I grade as 'tough' [Load], five are diabolical (for example [Load] and the remaining are extreme (for example [Load].
Ruud's top 50k
Another set I use for testing is Ruud's top 50k. Ruud, from the Netherlands, was active in the early days of Sudoku and produced a great set of very tough puzzles which is a good benchmark. We need to contrast the 17 clue sample with puzzles of a higher density. After discarding all trivial puzzles (a few hundred) we get this chart:
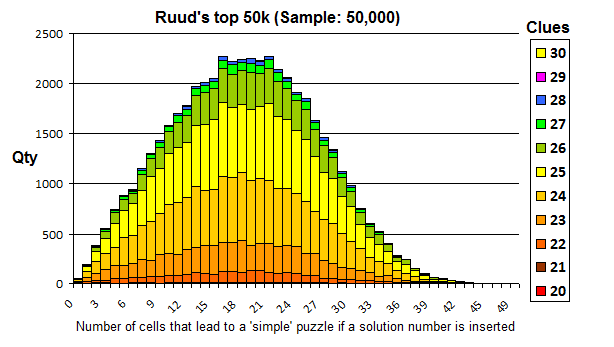
An even more perfect Bell Curve and this clearly shows that clue density is no clue to the difficulty of the puzzle or the number of cells that could lead to trivial puzzles. Only 33 puzzles are 'zero' puzzles and I include one in the example near the top of the page.

An even more perfect Bell Curve and this clearly shows that clue density is no clue to the difficulty of the puzzle or the number of cells that could lead to trivial puzzles. Only 33 puzzles are 'zero' puzzles and I include one in the example near the top of the page.
Level-2 Puzzles
For all the puzzles with zero cells that lead to trivial (Level-2) puzzles - I have tested them by inserting two clues. The number of ways that two clues can be inserted is rather large. If E is the number of empty cells then the number of ways to select two cells is the sum of the series 2 to E. In the case of a 30 clue puzzle there are 1325 ways to select two empty cells. In the case of a 17 clue puzzle there are 2016 ways.
I have tested all 118 level-2 puzzles and David Filmer's two puzzles are hands down winners:
I have tested all 118 level-2 puzzles and David Filmer's two puzzles are hands down winners:
- Unsolvable #28 just 9 out of 1711 (0.526%)
- Unsolvable #49 with 24 out of 1711 (1.4%)
Interestingly, a new puzzle by Arto Inkala which is in the Daily Telegraph claims to be the 'new hardest ever' but according to the this new metric it does not beat David Filmers two puzzles. It is a level 2 unsolvable with 79 out of a possible 1770 pairs of cells giving a 4.5% 'trivialization' rate. All the remaining unsolvables and extremes contain between 5% and 30% of pairs. I suspect this metric is a rough and ready approach compared to Arto's more sophisticated scoring method.
You can load Arto Inkala's puzzle from this link
I think if there is a puzzle so tantalizingly close to a a level 3 (requiring three insertions) then a level-3 might just be possible. I am reminded of the Rubik's Cube where it has been determined that no position is more than twenty moves away from a solution. Given the tiny space that puzzle operates in the idea that the puzzle can collapse with a few additional numbers placed shouldn't be surprising. But remember, the cut-off point for triviality is arbitrary. Why did we stop at Intersection Removal? If you stop at Quads you will get a different results.
This could be a useful tool for distinguishing between unsolvables and comparing extremes so I will explore further. Looking forward to hearing from everyone else.
Andrew Stuart
A Level-3 Example
Update: 5th of July
Many thanks to Ronk who writes below. He has alerted me to a small number of Level-3 puzzles. You can load the best one here. This is pretty impressive. So, neither 1 nor 2 insertions in any place or combination will render this puzzle trivial. Enlarging the search space I've tested all 32,509 combinations of three insertions and 725 will break the puzzle (the first is 2 in A2, 3 in A3 and 7 in D8) which is a tiny 2.2% success rate. Thanks Ronk!
Link to thead with links to useful catalogues of very hard puzzles here.
Many thanks to Ronk who writes below. He has alerted me to a small number of Level-3 puzzles. You can load the best one here. This is pretty impressive. So, neither 1 nor 2 insertions in any place or combination will render this puzzle trivial. Enlarging the search space I've tested all 32,509 combinations of three insertions and 725 will break the puzzle (the first is 2 in A2, 3 in A3 and 7 in D8) which is a tiny 2.2% success rate. Thanks Ronk!
Link to thead with links to useful catalogues of very hard puzzles here.


Comments
... by: Martin Pahlplatz
The link refers to the last “Unresolvable”, currently #580.
... by: L.D. den Boer
I've not yet encountered a puzzle my solver cannot solve. It finds the solution to David Filmer's #28 puzzle in 6 seconds, requiring 13,960 steps, with a maximum stack size of 13, maximum of 2 digits pushed at the same time, 937 pushes and 932 pops. Do you know of any more difficult puzzle than this one?
Lennert
... by: ronk
1 . . | . . . | 7 . .
. . 7 | 1 . 9 | . . .
6 8 . | . 7 . | . . .
-------+-------+-------
. . 1 | . 9 . | 6 . .
. . . | 3 . . | . 2 .
. 4 . | . . . | . . 3
-------+-------+-------
. . 8 | . 6 . | 1 . .
5 . . | . . . | . 4 .
. . . | . . 2 | . . 5
... by: DirkSJ
Of your zero's, how many are solvable using ALL current techniques with one well chosen filled in cell?
If there are any that remain "unsolvable" with any added known then that is an even harder benchmark. This would lead to a hierarchy of:
- trivial after 1 cell (all your non-zeros)
- solvable after 1 cell (your zeros that can be solved by advanced methods after 1 cell)
- unsolvable after 1 cell (zeros that are still unsolvable after 1 cell)
- trivial after 2 cells (assuming the current theory that all are trivial after 2 cells is true)
It's possible also that the "unsolvable after 1 cell" set has no puzzles in it. Perhaps using all current techniques this is an empty set.
Rephrasing your question, what is the lowest score/grade puzzle we can make with the addition of one extra clue? I agree it is possible some will continue to be unsolvable - just maybe - but we have so few to work with to check. There are 4 in the unsolvable list, 46 in Klaus's set, I think 9 in the 17 clue set and about 80 in the top 50k set. I will test them however, and see what it gives us. Whether it's meaningful with such as small sample I don't know, but fun to try.
Side issue: Bowman's Bingo muddies the waters a lot and I'm wondering what to do with this strategy. It is implemented and available but its trial and error. When I make puzzle for publication I don't include BB when grading so this strategy doesn't affect extremes. But I include it when searching for unsolvables because I don't want that step available for people to solve - or for the solver to finish it with that step.
I'll post again when I have results
Cheers
Andrew - [Del]