BUG+1
BUG stands for Bi-Value Universal GraveThe principle behind BUG is the observation that any Sudoku where all remaining cells contain just two candidates is fatally flawed. There would have been a last remaining cell with three candidates. The odd number that couldn't be paired with another cell would have to be the solution for that cell in order to prevent the bi-value 'Graveyard'.
Thanks to Peter Hopkins for re-engaging me with BUG (July 2015). He has found the original discussion which goes back to November 2005. Here is the link. From my testing of large data sets I believe that every instance of BUG can be solved by an XY-Chain. Hence it is positioned just before that strategy in the solver - it is an easy solution if you can recognise the pattern. Other simpler strategies may also do the same job but not as completely as XY-Chains.
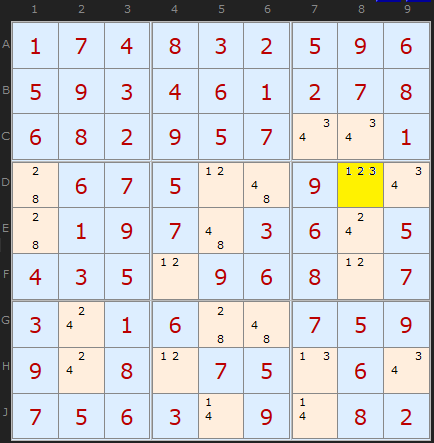
The BUG cell is D8.
Removing candidate 1 from the cell does not create a deadly pattern, since candidate 1 would appear in Row D, Column 8 and Box 6 just once. Removing candidate 2 results in:
- Row D containing candidates 1, 2, 3, 4 and 8 all exactly twice.
- Column 8 containing candidates 1, 2, 3 and 4 all exactly twice.
- Box 6 containing candidates 1, 2, 3 and 4 all exactly twice.
- Every other unit containing unsolved cells in which all candidates appear exactly twice.
Thus, in order to kill the BUG, D8 must be 2.
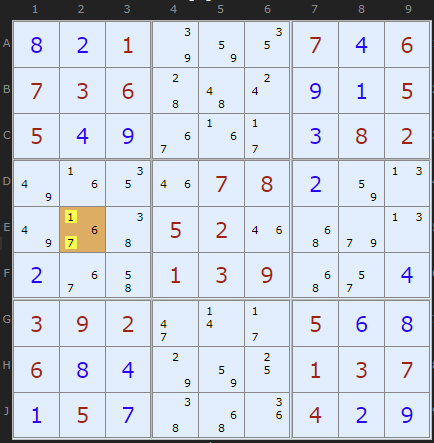
It is possible for the BUG to exist in a sea of bi-value cells, such as this one discovered by Klaus Brenner. It is also notable for having two whole boxes with only bi-value cells.
Sudoku X BUGs - careful!

While testing I found this interesting false positive.
This is a Sudoku X puzzle so there are extra constraints on the diagonals. But the remaining candidates form a BUG pattern. Or do they? A9 contains 5,7,9. How to decide which candidate is the solution?
At this point I was not checking the diagonals so I missed that 9 would leave a single 9 in the diagonal on F4. So none of the candidates 5,7 and 9 qualify for the criteria even though 5 is the solution to A9.
The puzzle can be resolved with Simple Colouring on 5.
BUG Exemplars
These puzzles require the Bi-Value Universal Grave strategy at some point.Only the first is somewhat trivial. They make good practice puzzles.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Charles R Cochems
1) is the unsolved number of cells odd? if not you do not have a situation you can apply this to.
2) is there exactly ONE cell left with three? If not, you need to make more eliminations.
3) are all the other numbers penciled in in no more than 2 cells in each row, column or box? If no, you need to eliminate more until you are within the limits.
4) this all being true, one of the numbers in that cell will be in one row, column, and box three times instead of two. This is the number that has to be placed there to kill the BUG, and it will create at least four naked singles. two in the row, and two in the column. I believe it is always four, because the only way I see for there to be three in a box, row, and column is if the box and row or column share a set of 3 of the number.
... by: domP
Can you confirm ? If not, maybe you have a counter-example ?
So we need to check the number of solutions before using 'BUG'.
As I don't know uniqueness of solution, I never use 'BUG'. It's the same as all the unique rectangle methods.
Is it a correct method to check a new puzzle ?
It seems also that, if we put this BUG test, after XYchains, it will never be usefull. Right ?
Thanks a lot for all explainations.
DomP
... by: NeutrinoAnt
... by: Kasper D
... by: Jonathan Handojo
... by: Jan
... by: David Filmer
2..4..5.1..1.38.9..3....7.8.7...2..3.6..9...5.4......9..4....6.62.3..8..81..47...
I entered it into the Brent Knoll News February 2019 edition and called it Valentine, as the clues are in the shape of a heart with a Cupid's Arrow piercing it!
All the other illustrations of a BUG (above) had many more. Can anyone else find a BUG with less than 13 unsolved cells?
... by: Pieter, Newtown, Australia
AS a person reading about BUG for the first time may I make these suggestions to make this brief explanation clearer:
1. As noted by strmckr on 26/10/15, BUG "requires knowledge of unique rectangles and deadly patterns to apply its technique correctly". Since BUG is applied before URs in the solver, I think a reference should be made (in the first paragraph) to UR's strategy explanation for the novice to get an explanation of "deadly patterns".
2. "Removing candidate 1 from the cell ... " OR candidate 3
3. Adding a numbered point 5. something like "Hence the whole of the unsolved part of the puzzle becomes a deadly bi-value pattern". Not obvious to a BUG novice. ;-)
All the best for the new year!
Ciao
Pieter
... by: strmckr
finned/sashimi x-wing { fish pattern's }
out side of that it requires knowledge of unique rectangles and deadly patterns to apply its technique correctly.
Bug
http://forum.enjoysudoku.com/the-bug-bivalue-universal-grave-principle-t2352.html#p14899
bug lite
http://forum.enjoysudoku.com/between-uniqueness-and-bug-bug-lite-t3056.html
for reference to the other type of uniqueness based solving techniques also not covered on this site
http://forum.enjoysudoku.com/collection-of-solving-techniques-t3315.html
look up:
reverse bug,
reverse bug lite
mug
here is another one that is surprising powerful but often missed,
the unique rectangle 1.1
http://forum.enjoysudoku.com/how-do-ars-arise-t31045.html#p226670
{there is early posts this one sums it up the best}
U.R 1.1
Definition: an a/b/b/a pattern in a solution grid is anything isomorphic to that shown below:
Code: Select all
. . . | .
a . . | b
b . . | a
---------+---
. . . | .
Fact: if a solution grid (not necessarily unique) contains an a/b/b/a pattern on four unclued cells, C, then C=b/a/a/b is also a solution.
Theorem: if a puzzle-in-progress (that does not necessarily have a unique solution) has pencilmarks as shown below on four unclued cells then the bottom right value resolves to '3':
Code: Select all
. . . | .
1 . . | 2
2 . . | 13
---------+---
. . . | .
Proof: suppose to the contrary the bottom right value resolves to '1'. Then (vacuously) the solution grid contains the 1/2/2/1 pattern on four unclued cells, C. So, by the Fact above, C=2/1/1/2 is also a solution. But wait! - the pencilmarks do not allow that other solution - contradiction.
denis_berthier wrote:
Thanks, RedEd, for this very smart proof.
Before it, UR1.1 was only a conjecture, a matter of belief or disbelief. It is now a valid theorem (we'll see later under what implicit conditions). It shows that a short and clean proof can do what pages of repeated but unsustained claims can't.
... by: mike
... by: Strmckr
Which are easier to spot then xy wings and even this.
Not to mention bugs and bug lite patterns only function based on uniqueness assumed.
... by: Brett Yarberry
The initial position of the board (loaded in solver) is: LOAD HERE
... by: Arthur Lurvey
I got it from http://homepages.cwi.nl/~aeb/games/sudoku/solving18.html. It can be solved using other methods, but they are of the diabolical class. So this makes for a good application of this technique.
Art
... by: Peru Boro
... by: Sean Forbes
Thanks. Sean
... by: Harmen Dijkstra