Cage Unit Overlap
Captured Candidates
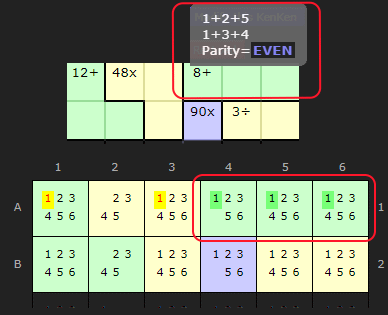
An example is provided on the right. 8+ in a 3-cage can be 1-2-5 or 1-3-4. Since 1 is necessary in both it can't exist elsewhere on the row.
Captured Candidates + Hidden Pairs/Triples will eliminate the same candidates as KenKen Combinations + Naked Pairs/Triples. They are two sides of the same coin. It is arbitrary which comes first but there has to be one order.
Cage Unit Overlap as used later will compute the candidates based not just on the clue and cage size but what candidates remain after other eliminations. This can be quite hard to do mentally so it is down the list.
Type 1
This is an important Killer Sudoku strategy which I have placed at the start of all the more complex strategies in the solver because it is so useful and very easy to spot. It is related to Intersection Removal. Whereas IR is the overlap of rows/columns with boxes, this is the overlap of 'cages' with rows, columns and boxes.
Each 'cage' is made up of one or more 'combinations' - sets of numbers that total the cage clue. If you can find a candidate number inside that cage that is not found elsewhere on the row, columns or box the cage is aligned on, then you know that number must appear in the cage. That part is self-evident since, in the solver at least, these numbers are displayed. Given that number is true, we can remove all combinations which omit that number. Often that means we can remove a bunch of numbers.
Each 'cage' is made up of one or more 'combinations' - sets of numbers that total the cage clue. If you can find a candidate number inside that cage that is not found elsewhere on the row, columns or box the cage is aligned on, then you know that number must appear in the cage. That part is self-evident since, in the solver at least, these numbers are displayed. Given that number is true, we can remove all combinations which omit that number. Often that means we can remove a bunch of numbers.
Example 1 (Link)
In the first example below, two such Cage/Unit Overlaps occur. The 2-cell cage with the red box has a clue of 14, which means the two combinations (visible if you hover over the cage on the solver) are {5,9} and {6,8}. The 6s in the cage are unique to that cage and the cage is entirely inside the box. So the only combination that fits is {6,8}. Hence we can remove 5s and 9s from the cage. In fact, since {6,8} is the only combination left both those numbers must fit in the cell and ALL other candidates can be removed, so the 4s and 3s can also go.
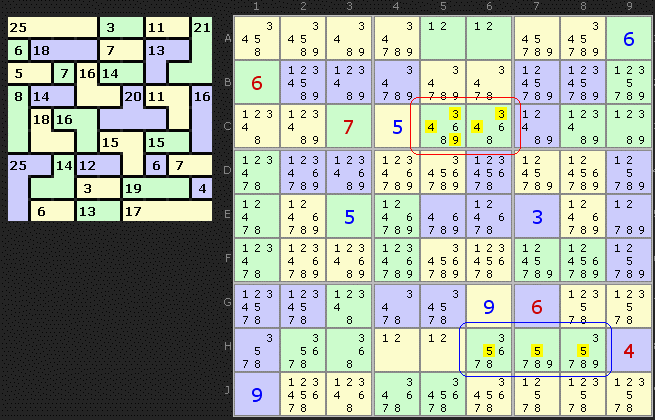
The blue ringed cage, a 3-cell with a clue of 19 gives us five different combinations. But the 9 in that cage is unique to both the cage and row H, so only the combinations with 9 in them are valid. {4,7,8} and {5,6,8} are not possible. Of the remaining candidates, the 5s can be removed.
In the first example below, two such Cage/Unit Overlaps occur. The 2-cell cage with the red box has a clue of 14, which means the two combinations (visible if you hover over the cage on the solver) are {5,9} and {6,8}. The 6s in the cage are unique to that cage and the cage is entirely inside the box. So the only combination that fits is {6,8}. Hence we can remove 5s and 9s from the cage. In fact, since {6,8} is the only combination left both those numbers must fit in the cell and ALL other candidates can be removed, so the 4s and 3s can also go.

The blue ringed cage, a 3-cell with a clue of 19 gives us five different combinations. But the 9 in that cage is unique to both the cage and row H, so only the combinations with 9 in them are valid. {4,7,8} and {5,6,8} are not possible. Of the remaining candidates, the 5s can be removed.
Example 2 (Link)
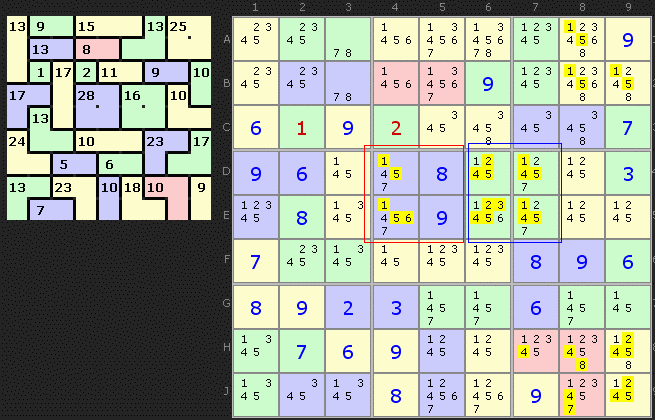 In this second example, five Cage/Unit Overlaps have been found. Taking just the centre one as an example, the red ringed 4-cell cage has a clue of 28 - the combinations being {4,7,8,9} and {5,6,8,9}. 7 is, however, unique to the cage and the centre box, so only the first combination can be valid. 5s, 6s and other numbers not in that combination (the 1s) can be removed.
I'll leave it to you to show how the other four cages have similar eliminations.
Overall, most Killer Sudoku puzzles will have at least one example of this strategy so they are well worth looking out for, and often you can reduce the puzzle with this method while looking into the cages with multiple combinations. Keep an eye out on the rows, columns and boxes you are studying.
In this second example, five Cage/Unit Overlaps have been found. Taking just the centre one as an example, the red ringed 4-cell cage has a clue of 28 - the combinations being {4,7,8,9} and {5,6,8,9}. 7 is, however, unique to the cage and the centre box, so only the first combination can be valid. 5s, 6s and other numbers not in that combination (the 1s) can be removed.
I'll leave it to you to show how the other four cages have similar eliminations.
Overall, most Killer Sudoku puzzles will have at least one example of this strategy so they are well worth looking out for, and often you can reduce the puzzle with this method while looking into the cages with multiple combinations. Keep an eye out on the rows, columns and boxes you are studying.
 In this second example, five Cage/Unit Overlaps have been found. Taking just the centre one as an example, the red ringed 4-cell cage has a clue of 28 - the combinations being {4,7,8,9} and {5,6,8,9}. 7 is, however, unique to the cage and the centre box, so only the first combination can be valid. 5s, 6s and other numbers not in that combination (the 1s) can be removed.
I'll leave it to you to show how the other four cages have similar eliminations.
Overall, most Killer Sudoku puzzles will have at least one example of this strategy so they are well worth looking out for, and often you can reduce the puzzle with this method while looking into the cages with multiple combinations. Keep an eye out on the rows, columns and boxes you are studying.
In this second example, five Cage/Unit Overlaps have been found. Taking just the centre one as an example, the red ringed 4-cell cage has a clue of 28 - the combinations being {4,7,8,9} and {5,6,8,9}. 7 is, however, unique to the cage and the centre box, so only the first combination can be valid. 5s, 6s and other numbers not in that combination (the 1s) can be removed.
I'll leave it to you to show how the other four cages have similar eliminations.
Overall, most Killer Sudoku puzzles will have at least one example of this strategy so they are well worth looking out for, and often you can reduce the puzzle with this method while looking into the cages with multiple combinations. Keep an eye out on the rows, columns and boxes you are studying.
Type 2
If Type 1 above is related to Box Line Reduction, then you'd recognize that Type 2 will look like Pointing Pairs, it's opposite. Credit to Caleb Andrews for finding this example and stating the logic so elegantly.
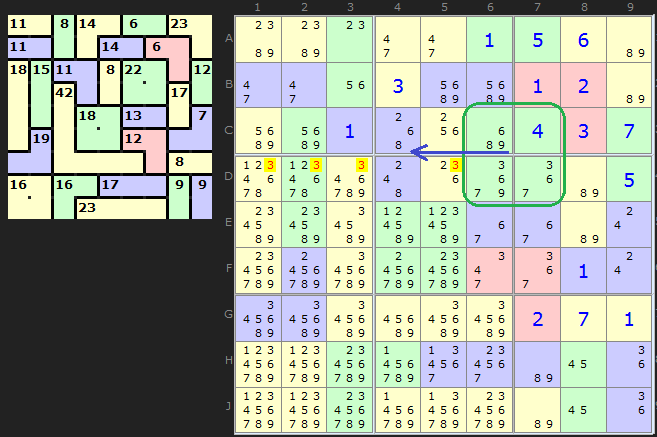
In this puzzle (also used in the Innies/Outies example) we consider the 4-cage in a square CD67. Because the 4 is fixed in C7 we only need to consider the combinations that have 4, but
1489 <- no 1 left in the cage
2479 <- no 2 left in the cage
3469
3478
4567 <- no 5 left in the cage
so we are left with two combinations. Both contain 3 and 4. 4 is not helpful as we've already placed it, but look where 3 fits in the cage. It can only go in D6 and D7. That makes 3 a certainty in those cells. So it acts like a Pointing Pair aligned on the row. We can remove 3 from D1235.
There is another large example of this strategy in the same puzzle, on the big L cage starting on D3.

In this puzzle (also used in the Innies/Outies example) we consider the 4-cage in a square CD67. Because the 4 is fixed in C7 we only need to consider the combinations that have 4, but
1489 <- no 1 left in the cage
2479 <- no 2 left in the cage
3469
3478
4567 <- no 5 left in the cage
so we are left with two combinations. Both contain 3 and 4. 4 is not helpful as we've already placed it, but look where 3 fits in the cage. It can only go in D6 and D7. That makes 3 a certainty in those cells. So it acts like a Pointing Pair aligned on the row. We can remove 3 from D1235.
There is another large example of this strategy in the same puzzle, on the big L cage starting on D3.
Type 3
The third theme of Cage Unit Overlap considers cages of size N with N remaining numbers. All numbers are necessary to the cage (locked set). Then, if any one or more of those candidates are exclusive to any row, box or column they point along that unit to candidates which can be eliminated. On small straight cages this will often be a Naked Pair, Triple etc and dealt with earlier. But for larger cages that 'dog-leg' it is possible some remaining candidates will be on one part of the 'leg' and aligned with a unit.
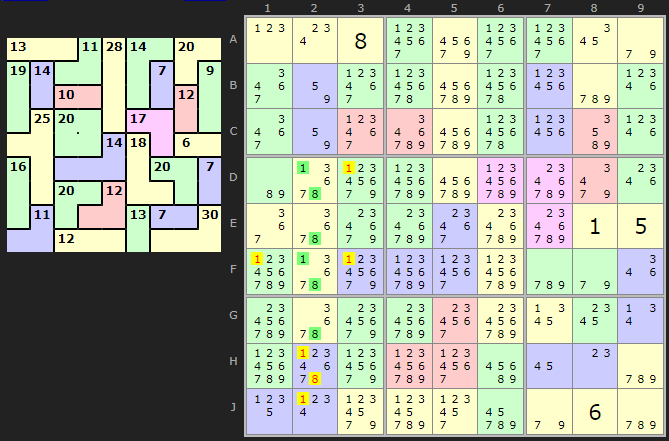
In this example the 5-cell with 25+ starting on D2 has {1,3,6,7,8} to fill all cells. But 8 is exclusive to column 2 and 1 is exclusive to both column 2 and box 4. So eliminations are made on those units.
Load this example or From the start [Added Jan 2025]

In this example the 5-cell with 25+ starting on D2 has {1,3,6,7,8} to fill all cells. But 8 is exclusive to column 2 and 1 is exclusive to both column 2 and box 4. So eliminations are made on those units.
Load this example or From the start [Added Jan 2025]
Bi-Value attack on a cage
Another type of elimination I've chosen, a bit arbitrarily, to insert into the search at this strategy point is to compare a cage with a bi-value cell. This was a tip from Ivar Ling.
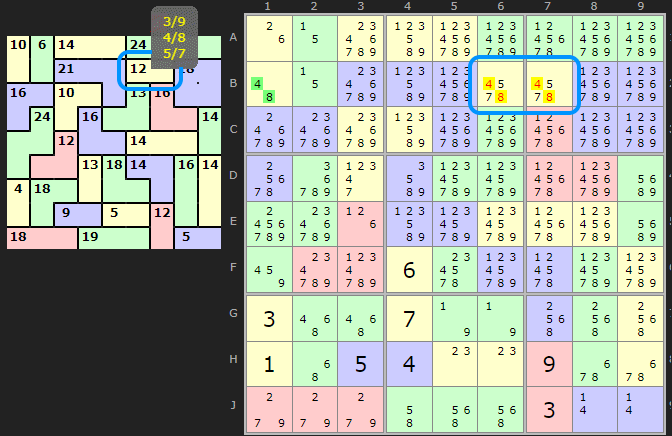
In this puzzle the 2-cage with a sum of 12 can only be {4/8} or {5/7} (with {3/9} already removed). Now a bi-value cell B1 can see all the cells in this cage and it contains a pair of candidates which matches one of those combinations. Since B1 must be either 4 or 8 it removes {4/8} combination from the cage. This will be reported as
Cage/Unit Overlap
CAGE vs BIVALUE: the cage starting on B6 has combinations which are ruled out by bi-value cell B1 which can see all cells in the cage, so
- we can remove 4/8 from B6
- we can remove 4/8 from B7
Update 26 August 2025: Cages longer than two cells can now be detected with this pattern. This is an example.

In this puzzle the 2-cage with a sum of 12 can only be {4/8} or {5/7} (with {3/9} already removed). Now a bi-value cell B1 can see all the cells in this cage and it contains a pair of candidates which matches one of those combinations. Since B1 must be either 4 or 8 it removes {4/8} combination from the cage. This will be reported as
Cage/Unit Overlap
CAGE vs BIVALUE: the cage starting on B6 has combinations which are ruled out by bi-value cell B1 which can see all cells in the cage, so
- we can remove 4/8 from B6
- we can remove 4/8 from B7
Update 26 August 2025: Cages longer than two cells can now be detected with this pattern. This is an example.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: YBB