Cage Comparison
Example 1
The first cage comparison strategy consists of detecting if one cage has combinations which, if set as the values for that cage, will leave another cage without any valid sets of numbers. The second target cage has to be accessible, i.e. wholly 'seen' by the first cage. And that means all the cells in both cages must be mutually 'seen' (looking along the row, column or within the same box).
Load into solver
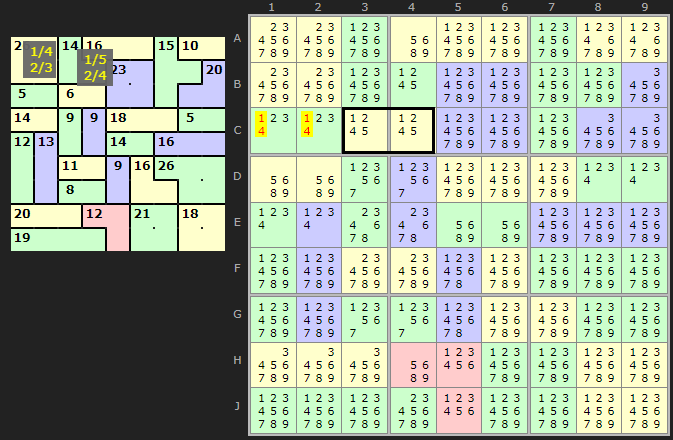
In the first example the 2-cage on C1 has combos {1/4} and {2/3}. Along the row is a 2-cage starting at C3. This has been reduced to {1/2/4/5} in both cells leaving {1/5} and {2/4} as possible combiates. Since 1 and 4 in the first cage invalidate both these options 1 and 4 cannot be part of the cage on C1.

Load into solver
In the first example the 2-cage on C1 has combos {1/4} and {2/3}. Along the row is a 2-cage starting at C3. This has been reduced to {1/2/4/5} in both cells leaving {1/5} and {2/4} as possible combiates. Since 1 and 4 in the first cage invalidate both these options 1 and 4 cannot be part of the cage on C1.
Example 2
The second example shows this strategy is not confined to pair cages but they will be the most common. Here two 3-cages within the same box are compared. Usefully they have the same clue but on the face of it have a lot of combinations.
Load into solver
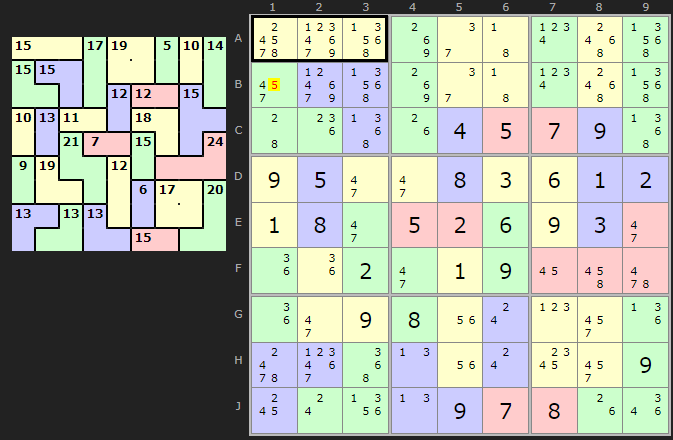
So the cage starting on B1 has been reduced the most and {2/5/8}, {2/6/7} and {3/4/8}. But check out {2,5,8}. If that is the solution then it affects the A1 cage:
A1 cage combo 159
A1 cage combo 168
A1 cage combo 258
A1 cage combo 267
A1 cage combo 348
A1 cage combo 456
So no combination works. We can therefore remove 5 from cage B1.

Load into solver
So the cage starting on B1 has been reduced the most and {2/5/8}, {2/6/7} and {3/4/8}. But check out {2,5,8}. If that is the solution then it affects the A1 cage:
A1 cage combo 159
A1 cage combo 168
A1 cage combo 258
A1 cage combo 267
A1 cage combo 348
A1 cage combo 456
So no combination works. We can therefore remove 5 from cage B1.
Example 3
Lets look at JohnNoneDoe's latest example from 2019. Load into solver
As he writes, the 12-in-2 cage at AB9 must be {9/3} or {8/4}. Thus the 8-in-3 cage at ABC8 cannot be {1/3/4} - it must be {1/2/5} and "the solution is straightforward".

As he writes, the 12-in-2 cage at AB9 must be {9/3} or {8/4}. Thus the 8-in-3 cage at ABC8 cannot be {1/3/4} - it must be {1/2/5} and "the solution is straightforward".


Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Mika
... by: Ahydul
... by: JohnNoneDoe
The solver cannot proceed further even with all strategies enabled.
Consider the cage starting at d5 and the 1-cell pseudo-cage b5; the cage at d5 cannot be 189 because that would leave b5 empty. Solution is straightforward if the 1's are removed from cage d5.
I looked at the board given in the example and it looks like John is referring to the 18 cage on *D4* instead, since 1+8+9=18 (he must have made a typo).
A cage vs bivalue (which is supposed to be implemented in the solver) would compare this cage with B4, which is a bivalue cell with only 8 and 9, removing 1/8/9 as a possibility and subsequently removing 1 from the cage completely, but your solver does not see this.
This is either a bug or an incomplete implementation.
Manually removing 1 from the cage allows the solver to solve the puzzle completely.
... by: JohnNoneDoe
There is a Killer Sudoku board I would like you to look at
Click on this link:
http://www.sudokuwiki.org/killersudoku.htm?bd=112212212223313412112213413113313443124412241322313311312312211212313322214412211,060012004508000812090009000015270000240017000000000013000003000000000000002706000013000022140000170006000000001600000013000000080000000009001300000012000009001200
The solver fails but the puzzle is easily solved using cage comparison.
The 12-in-2 cage at ab9 must be 9,3 or 8,4. Thus the 8-in-3 cage at abc8 cannot be 1,3,4; it must be 1,2,5 and the solution is straightforward
... by: JohnNoneDoe
Click on this link
The solver fails on this board. It can be easily solved using what I think is an application of cage comparison. The 13-in-2 cage at a78 cannot contain 6,7 because of the 15-in-2 cage at a34. Thus the 5 cell innie in box 3 summing to 45-13-14=18 must contain a 7, 18-in-5 is 12357.
... by: JohnNoneDoe
There is a Killer Sudoku board I would like you to look at
Click on this link:
http://www.sudokuwiki.org/killersudoku.htm?bd=112212211213313312244212442114232411112131211232121232231121132132232231111333111,190009001808001700100006000012000005001500070006220000200000001100002100000015270018070000051100000600001814000000000000000000190009002511000014000000000000000000
The solution is straightforward when one notes the hidden pair 1,4 in 5hj and 5fg which leads to a hidden pair 8,9 in 5abc and 6b. I think think this observation would be a result of what I think of as cage comparison.
Looking at the board, I understood what John is trying to say.
The 6-in-2 cage at F5 and the effective 10-in-2 cage at H5 (a 25-in-4 reduced with 7 and 8 as solved numbers) both require either 1 or 4:
6-in-2 at F5: 1/5, 4/2
10-in-2 at H5: 1/9, 4/6 (all other combinations are removed)
Either:
a. 1 is true in F5 cage, and 4 is true in H5 cage,
b. 4 is true in F5 cage, and 1 is true in H5 cage.
This virtually forms a naked (not hidden!) pair, allowing 1 and 4 to be removed in all other cells in column 5 (ABCDE5). Sudopedia notes this strategy as Killer Pairs.
I don't understand the 2nd point John states, but the solver can actually solve this puzzle from this point onwards now. (Interestingly, a grouped X-cycle is required to proceed, which is exceedingly rare to find in a Killer.)
... by: JohnNoneDoe
... by: Thinkist
Also, the X-Wing strategies and those below it are useless (or at least really rare). Same for KenKen and KenDoku.