Innies and Outies
This is a fundamental strategy for Killer Sudoku puzzles of any difficulty. It is extremely versatile and worth looking out for it at every stage. Fortunately it only requires simple addition and spotting a certain type of pattern.
Since the basis of the puzzle is Sudoku, each row, column and box will eventually have solutions which always add up to 45. If we can identify a group of cages which almost covers a unit (or more than one unit) but has one cage either sticking out (an Outie) or poking in (an Innie) we can make some very useful deductions.
I'm going to refer to Block as any set of adjacent rows, columns and boxes we can use in concert, but also a block could be just one row, column or box. Innies and Outies occur naturally because cages often line up with the Sudoku elements but in the middle and end game you can split the cages that contain solutions and create new useful blocks that were not available at the start.
I've deliberately split this strategy in the solver between the easier-to-spot single cell Innies and Outies and the multiple cell ones - which require more mental calculation and therefore go further down the strategy order. Lets plunge in.
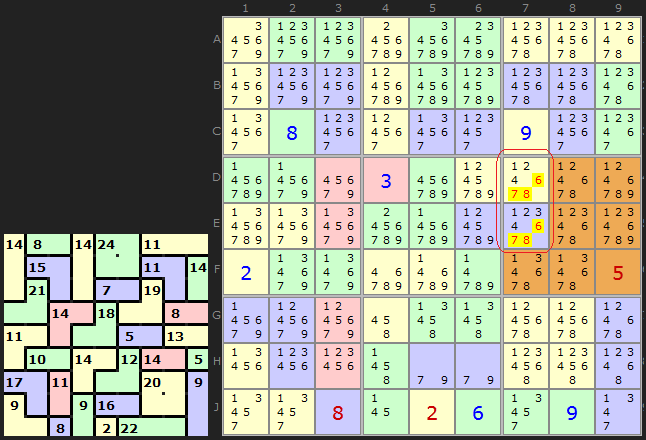
You will see two examples in the first diagram. This Killer Sudoku is symmetrical - which will often yield a double Innie and Outie.
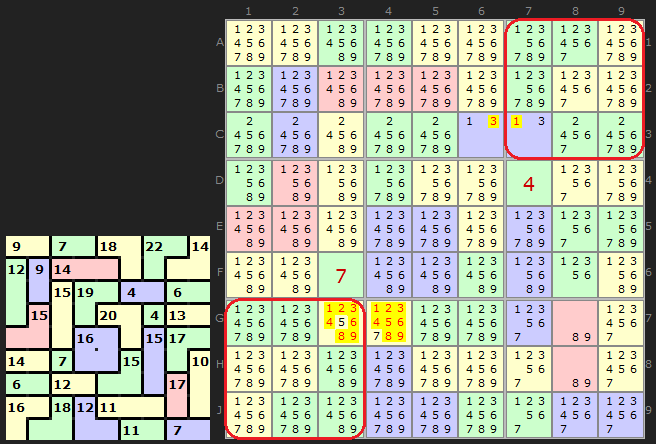
The two red rings surround boxes 3 and 7. Both boxes contain complete cages apart from one two cell cage. Lets add up the clues for complete cages in each box. We have:
Box 3 = 22 + 14 + 6 = 42
Box 7 = 6 + 16 + 18 =40
We therefore know that Box 3 is missing 3 which can only go in C7 and Box 7 is missing 5 which must go in G3. Because we are dealing with simple 2-cell cages we get the other halves as well.
Since the basis of the puzzle is Sudoku, each row, column and box will eventually have solutions which always add up to 45. If we can identify a group of cages which almost covers a unit (or more than one unit) but has one cage either sticking out (an Outie) or poking in (an Innie) we can make some very useful deductions.
I'm going to refer to Block as any set of adjacent rows, columns and boxes we can use in concert, but also a block could be just one row, column or box. Innies and Outies occur naturally because cages often line up with the Sudoku elements but in the middle and end game you can split the cages that contain solutions and create new useful blocks that were not available at the start.
Single Cell Innies and Outies
I've deliberately split this strategy in the solver between the easier-to-spot single cell Innies and Outies and the multiple cell ones - which require more mental calculation and therefore go further down the strategy order. Lets plunge in.
You will see two examples in the first diagram. This Killer Sudoku is symmetrical - which will often yield a double Innie and Outie.

The two red rings surround boxes 3 and 7. Both boxes contain complete cages apart from one two cell cage. Lets add up the clues for complete cages in each box. We have:
Box 3 = 22 + 14 + 6 = 42
Box 7 = 6 + 16 + 18 =40
We therefore know that Box 3 is missing 3 which can only go in C7 and Box 7 is missing 5 which must go in G3. Because we are dealing with simple 2-cell cages we get the other halves as well.
If we proceed a little further down the puzzle we get another useful Innie and Outie, this time made up of two columns. Since we are using two columns, the number we are interested in arriving at is 90. On the left hand side ringed in red, the cages are 9 + 12 + 9 + 15 + 14 + 6 + 16 = 81, so 9 has to come from the 3-cell cage totalling 18. 9 can be placed in J2. As the puzzle is symmetrical a similar technique can be applied to the other side.
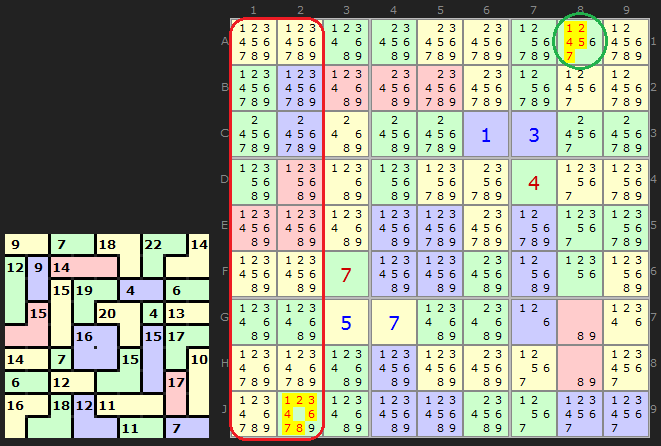
Just to show that blocks can be 2 by 2 boxes as well this tough Killer has this step.
Killer Innies (2+ cells)You can Load it here and see the example.
OUTIE 'Pen' Pseudo-cage: Boxes 5,6,8,9.. adds up to 180 but all cages
add up to 193 leaving 13 in outie cells. Given the available combinations...
- we can remove 1/2/5 from F3 (only 4 is possible)
- we can remove 1/9 from J2 (only 4/5 is possible)
- we can remove 1/9 from J3 (only 4/5 is possible)
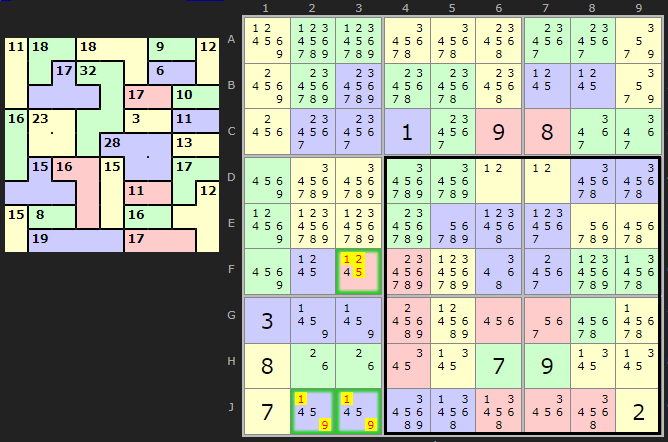
1 Innie + 1 Outie
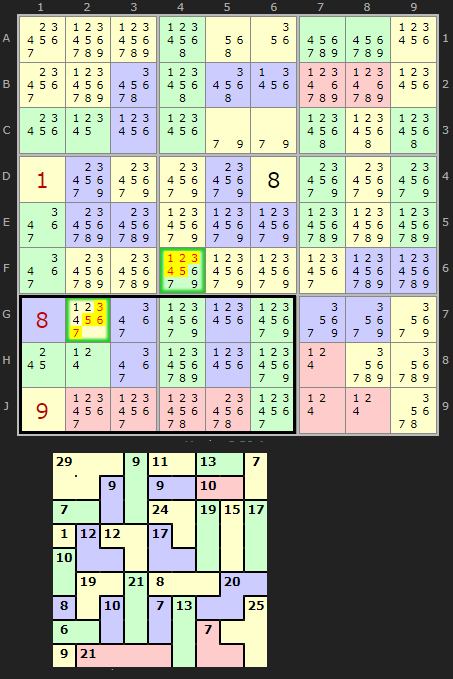
For this documentation page I've picked a relatively easy puzzle with eleven instances so well worth stepping-though on the solver. You can load it from here.
This block of two boxes must add up to 90 (45+45). The pattern we want is one innie cell, in this case G2 and one outie cell, here F4. The remaining cells of the outie cage are inside the block. The remaining cells of the innie cage are outside. We are going to add up all the cages entirely inside the block (which is 74) and then add the cage with the one cell outie F4. So 74+21 gives us 95. There is a difference of 5 (95 - 90). That means the solution for G2 must be 5 less than the solution for F4. This clears a lot of clutter since three pairs exist: 1 and 6, 2 and 7 and 4 and 9. Other candidates can be removed. The solver will return:
INNIE/OUTIE: A BLOCKS of 2 boxes (6 and 7)...
that contains a 1-cell innie G2 and a 1-cell outie
F4 must have solutions which differ by 5. (95-90=5). Therefore:
- we can remove 3/5/6/7 from G2
- we can remove 1/2/3/4/5 from F4
The Pseudo-Cage - multi-cell Innies
There is no restriction on the size of Innies and Outies - merely what is useful, and this goes back to combinations that fit certain cage sizes and have certain clues. Some cages are plane unhelpful, for example 24 spread over 4 cells. There are eight possible combinations from 1/6/8/9 to 4/5/7/8. 24 over 3 cells is much more interesting: 7/8/9 can be the only fit. So how about looking for Innies that are two, three - maybe four cells that have very low clues values or very high clue values.
The great idea about multi-cell Innies and Outies is that they don't have to fall over the existing cages the puzzle designer has made. You are creating new cages to restrict the candidates in the same way, but are made up on the spot from rows, columns and boxes - entities you know much add up to multiples of 45. I like to think of these are virtual or pseudo-cages - fleeting but useful.
Take this Killer Sudoku and the situation in box 6. Four cages are entirely inside the box and these have clues 8, 13, 14 and 5 which add up to 40. The remaining two cells in D7 and E7 therefore must add up to 5, to make a total of 45. It doesn't matter that these two cells are not in the same cage. D7 and E7 form a pseudo-cage of size 2 and a 'clue' of 5. That could be 1/4 or 2/3. Either way, we can remove 6/7/8/9 from those cells. It gets us closer.
The great idea about multi-cell Innies and Outies is that they don't have to fall over the existing cages the puzzle designer has made. You are creating new cages to restrict the candidates in the same way, but are made up on the spot from rows, columns and boxes - entities you know much add up to multiples of 45. I like to think of these are virtual or pseudo-cages - fleeting but useful.
Take this Killer Sudoku and the situation in box 6. Four cages are entirely inside the box and these have clues 8, 13, 14 and 5 which add up to 40. The remaining two cells in D7 and E7 therefore must add up to 5, to make a total of 45. It doesn't matter that these two cells are not in the same cage. D7 and E7 form a pseudo-cage of size 2 and a 'clue' of 5. That could be 1/4 or 2/3. Either way, we can remove 6/7/8/9 from those cells. It gets us closer.

Using Locked Sets to Split Cages
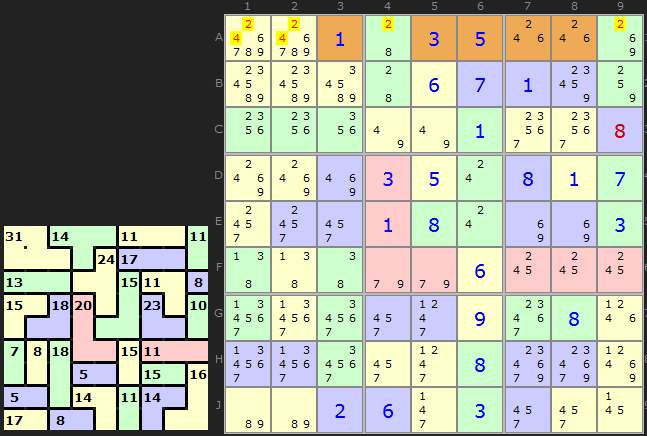
Here is a bolder four cell pseudo-cage using the top row as the block. We have one cages entirely inside the row (11) plus 1 and 3 (solutions in A3 and A5) gives 15. So 30 must be spread over four cells. 15+30=45. 30 is a good number since only 6/7/8/9 adds up to 30 so all the numbers below 6 can be removed. That gives us a solution of 8 in A4.

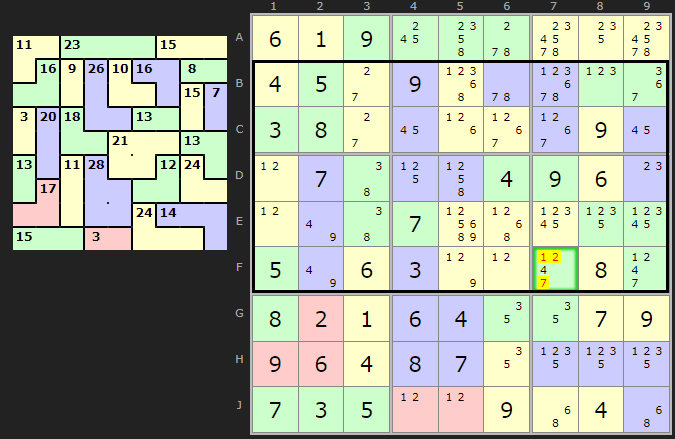
Just to show truly large 'blocks' can be useful, here is an example of five rows in combination. In this end-game situation all the solved in cells break up cages allowing for larger blocks and some Innie/Outie identification. Five rows at 45 each gives us 225. There is one cage that poked out. All cages in this block sum to 221 leaving 225-221=4 to fit in F7, therefore we can set F7 to 4
This is can be loaded here.
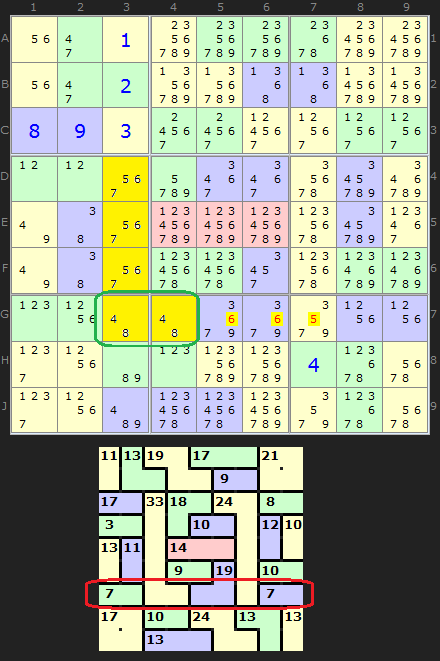
I was considering a puzzle idea sent to me by J Ignacio Fernandez from Spain when his idea kicked off another idea in my head. We were both looking at row G in the next puzzle. I got the notion that we could used Locked Sets to expand the number of Innies and Outies eliminations.
In the puzzle sent to me we have a long 5-cell cage valued at 33. The bottom two cells G3 and G4 contains a Naked Pair - a simple locked set. Because we know 4 and 8 must go in those cells (just not which way round yet) we can sum those values and let them contribute to the block we are making.
So adding 7 and 7 (first and last cages in row G) to the 12 (4+8) from G3 and G4 we get 26. So we need 19 to fit in the last three cells G567. Combinations of 19 in three cells means we can remove a candidate in each as shown on the diagram.
If the solver makes use of Locked Sets it will report this info alert:
(*note: the cage that includes C3 has been split to include it in the block)
New in version 2.12 (October 23th 2023)
Important update thanks to JohnNoneDoe from Arizona who supplies many examples in the comments, I have improved the Innies and Outies strategy. Particularly outies which he observed, do not need to obey the Dog-leg restriction on the pseudo-cell they create. This improvement has a large effect on hard Killers improving the hit rate (I hope). I have also changed how a block displays so as not to override the cell colours.
New in version 2.38 (August 28th 2025)
I wanted to document Herb Savage's excellent insight from his comment example. The diagram shows the position. Load example.
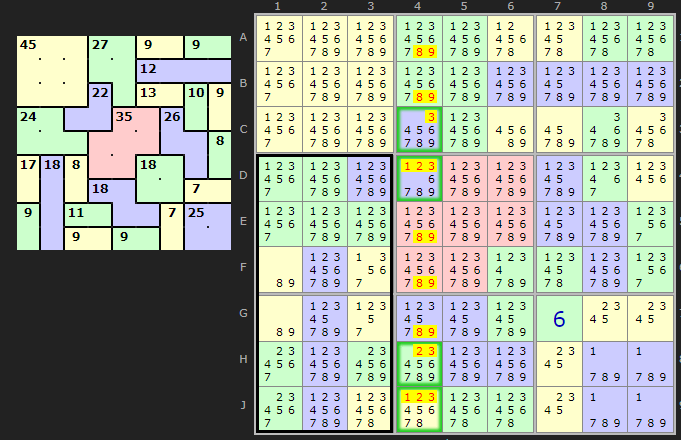
We have four cells CDHJ4 poking out of the block. While the block ads up to 90 the cages add up to 118 leaving 28 in outie cells. Four cells summing to 28 can only be achieve with {4/7/8/9} or {5/6/8/9}. Notice that 8/9 are in both combos so they are 'necessary'. Since the outie is aligned on a column that makes it effectively a Hidden Pair as we can eliminate in the rest of the column.
I wanted to document Herb Savage's excellent insight from his comment example. The diagram shows the position. Load example.

We have four cells CDHJ4 poking out of the block. While the block ads up to 90 the cages add up to 118 leaving 28 in outie cells. Four cells summing to 28 can only be achieve with {4/7/8/9} or {5/6/8/9}. Notice that 8/9 are in both combos so they are 'necessary'. Since the outie is aligned on a column that makes it effectively a Hidden Pair as we can eliminate in the rest of the column.
KenKen Innies and Outies
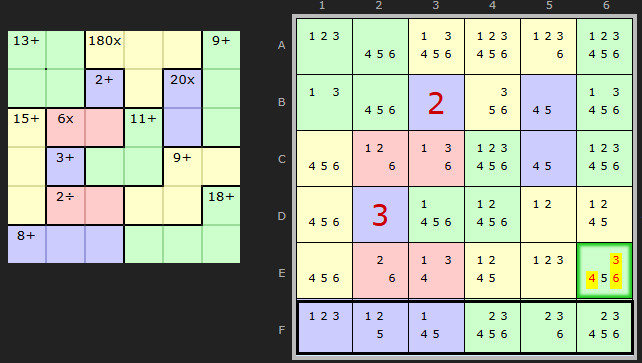
I can't remember the reason I excluded Innies and Outies from KenKen before 2025. There is some overlap with Rule of 21, Rule of Parity and Cage Comparison, but I think it was mainly the complexity of dealing with non-addition operators. Well, I had to tackle that to get further with those strategies just mentioned and now I've return to the "Killer Innies and Outies" code it is readily adaptable. I have slotted it into the ordering in a similar way to Mini Killer and Killer. Single-cell Outies being easy to find and easy to work out - these come high up the order. Two or more cells in an innie/outie come much later.
This first example comes a David Levy's tutorial puzzle. David was one of the promoters of KenKen when it was invented. The situation on the bottom row is an 8+ on F1 which allows us to work out that the whole row (Rule of 21) adds up to 21 and minus 8 leaves 13 to fit into the green cells F456. The are part of a cage with a clue of 18. Therefore 18 - 13 means 5 must be in E6.
Under the hood I'm treating any cage with a + symbol exactly as before and the code is the same as for Killer. However, only a minority of cages are addition so this is a limit. For other cages I look to see if there is one solution combination available for the remaining candidates in the cage. And thirdly, I take into account any solved cells.
The solver looks first for single rows and columns and them double, triple rows and columns up for four.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Herb Savage
Click on this link: Load Killer Sudoku
The first time it processes the outies of boxes 4 and 7, it displays the following message.
Killer Innies (2+ cells)
OUTIE 'Pen' Pseudo-cage: BLOCKS of 2 boxes (3 and 6)... adds up to 90 but all cages add up to 118 leaving 28 in outie cells. Given the available combinations...
- we can remove 1 from H4 (only 2/3/4/5/6/7/8/9 is possible)
- we can remove 1 from J4 (only 2/3/4/5/6/7/8/9 is possible)
It correctly identifies the total of 28 in 4 cells.
28 in 4 cells only has 2 possibilities
4/7/8/9 and
5/6/8/9
So, what I would do is remove 1/2/3 from the 4 cells
and remove 8/9 from the remaining cells in the column.
It removed the 1 from H4 and J4 but totally ignored the 1 in D4.
The second and last time it processes the outies of boxes 4 and 7, it displays the following message.
Killer Innies (2+ cells)
OUTIE 'Pen' Pseudo-cage: BLOCKS of 2 boxes (3 and 6)... adds up to 90 but all cages add up to 118 leaving 28 in outie cells. Given the available combinations...
- we can remove 2 from H4 (only 3/4/5/6/7/8/9 is possible)
- we can remove 2 from J4 (only 3/4/5/6/7/8/9 is possible)
Looking at the four cells when the solver has run out of known strategies. There is no 4 in any of the cells so now there is only one possibility 5/6/8/9. The two bottom cells each have a 3 and there are three 7's in the cells. If I remove 1/2/3/4/7 in those four cells and remove 5/6/8/9 from the remaining cells in the column the solver will complete the puzzle.
... by: Nene
Box 3 = 22 + 14 + 6 = 42
Box 7 = 6 + 16 + 18 =40
Where are these numbers coming from ?
... by: JohnNoneDoe
The solver fails to find the 3 cell outie in E2,F2,G2 adding to 68-45=23 and the rest is straightforward.
... by: Steven
I think the solver misses a 2 cell outie?
At the bottom three rows, the cages 32+20+27+24+14+24 have 2 cells extra.
So F1+F6=6
... by: Robert
... by: JohnNoneDoe
Click on this link: Load Killer Puzzle
The solver fails on this board. However, it can be easily solved using an extension of the concept of pseudo-cages.
In boxes 1,4,7 the set of cells a1-3, b3, d2, e23 must sum to 135-26-11-6-8-39-5=40. This set is not a pseudo-cage because it is not restricted by the killer cage convention; call such a set a pen. The complementary pen, cells a45, b5, e4, must sum to 28+9+26-40=23. In box 2 there is a pseudo-cage which must sum to 45-21-5=19. There is a relationship between the possibles, x, in cell e4 and the possibles, y, in cell c6; namely 23-x+y=19, x=y+4. The solver has determined that x is an element of {4,5,6,7}; since my editor does not have the "is an element of" symbol I write x=4,5 6,7. Similarly y=3,4,5,8. The only pair {x,y} which satisfies x=y+4 is {7,3} and the rest of the solution is straightforward.
It seems to me that this method is much easier for a pencil-and-paper solver than the exotic computer oriented strategies used by the solver.
I tested this particular example and no your solver doesn't currently solve the two cells that this analysis solves.
After looking at it a little more I realized there was a much simpler way to solve it.
Instead of looking at the 1,4,7 boxes look at the 1,2,4,7 boxes instead. Then you have two outies which sum to 16. These two outies are both in the same box so they are a true pseudo cage NOT a pen pseudo cage. Although it really doesn't matter in this case. Looking at the possibilities when the solver stops determines which is 9 and which is 7. Editing these two cells to the correct values and the solver finishes the puzzle.
Note, you can also take the 3,5,6,8,9 boxes and the two innies will solve for the same cells.
I also noted that in the solving comments you also say a lot of outies are pen pseudo cages that were actually just pseudo cages. In my mind a pen pseudo cage can have duplicates a non pen pseudo cage can't. If any pseudo cage is entirely in a row, column, box or existing cage then it is a full pseudo cage. If it isn't then the pen pseudo cage is not nearly as restrictive. The most common place I see pen pseudo cages are two outies on different sides of a box. For example, if the sum of the two cell Pen pseudo cage is 12 then you can't eliminate two sixes.
... by: GregMo
... by: JohnNoneDoe
"Killer Innies (2+ cells)"
with no elaboration and no brown emphasis on cells affected.
I cannot figure out the result.
Edit. The cells should now be highlighted in some way to make this clear
... by: Jonathan Clark
I get to 28 clues solved, and the next step is an "Innies/Outies (2-step)". It suggests some to remove, but it gives no details at all in the details box. I can see why one removal makes sense, but not the others. Perhaps there's a bug at this step?
INNIE/OUTIE: A block that must sum to 45 leaves 18 to fit in 3 cells belonging to cages not entirely within the block. Given the available combinations...
- we can remove 5/7 from C1 (only 2/6 is possible)
... by: JohnNoneDoe
There is a Killer Sudoku board I would like you to look at
Click on this link:
Load in Killer Solver
This board has a 2-cell innie in d5,f5 summing to 12. This creates a 2-cell pseudo-cage in c5,g5 summing to 9+11-12=8. Thus there can be no 4 in c5 or g5 and the solution is straightforward. The solver seems to require the distasteful use of Bowman Bingo.
... by: Fred
... by: Bernie
Click on this link
... by: PeteTy
*innie outie difference*
todays killer 20AUG2015 "moderate"
columns 1+2 have an innie outie difference of 8
unique 9 - 1 = 8
r1 c2 must be 1
r6 c3 must be 9
column 9 has the rather non helpful innie/outie difference of 1
r1 c8 cant have 9
r9 c9 cant have 1
combos left 89 78 67 56 45 34 23 12
other stuff in puzzle
col8+9 sum to 97 outie 7
r2 c7 = 7
box 1 has a dual outie of 12 (no cage convention)
r2c4 and r4c3 cant have 1or2 --- can have 3456789
find out after 30min of moderate that its the pair of 6's
col789 sum 124 dual innie 11 (cant have 1)
rows12345 dual outie 10 (cant have 5 )
so thats the ez stuff moderate in about an hour
... by: Jigancio
I'm sorry, but alas! this 'only' is not a solution, it gets stuck again a little later "run out of valid strategies"
Yes, of course, as I posted, g5+g6+g7=19, and the same g5+g6 plus f6 sum up also 19 (box).
Thus, necesarily g7=f6, that's the trick, and we can remove 4 from f6 and 9 from g7, what now leads to the solution (j7=9 and so on).
No doubt, you have improved the solver, but in my opinion it still lacks a routinary and effective way of detecting which squares are the same value in order to inmediately eliminate single candidates.
Sincerely yours
J. Ignacio Fernández
Thanks
... by: Steve K
... by: PeteTy
the thing that broke it for me was the c8-c9 triple innie 11
http://www.sudokuwiki.org/killersudoku.htm?bd=122111122113322212122113311332122212313313332213212113212212443231331211331131233,250900260000001300000007001000002000000600200009000000190000001700000015001518001209000000150000210008040014000000000000080000000920130011150700000000000000001000
so i loaded it in the solver
r78 single innie
n9 single innie
row 1-4 has dual outie 16 for a 7 9 pair
the solver spotted all those
box1 has a dual outie of 2
i noticed that before the singles but,
the solver never did spot it .. solver found the 1 to the south with some magic multiple cage interactions and exotic hard cage combinations
after it found the 1 to the east in the 7(2) cage,
it took several solve steps before it discovered the 6
I dont consider that particular combination to be a tough one ...
did notice the solver has:
Innies (2 to 4 cells)
doesnt have:
outies (2 to 4 cells)
a little thought will confirm outies dont have the cage convention (no doubles) while innies do
---------------------------------------------------
order of the steps the way i solve vs the solver
ill do cage splitting innies outies cage combinations way before hidden triples quads
way before y wings, colouring or pointing pairs
i really think the tough strategy on the killers shouldnt start before the normal sudoku tough strategy
perhaps move the blue ones (killer specific) to lower numbers
... by: Sharvan
... by: PeteTy
just look at the lack of the killer cage convention
a fun example (last above) gives N1+N2
an innie 36 or 90-(22+15+17)
a 9 cell pseudo-cage
it cant have 6 or 9 because they are required in the 22(3) and 17(3) cage
possibles
Digit Combinations - Can't Have Digits 69 Must Have Digits1234578
9 cell cage
36: 112345578* 122344578 123334578
Digits 1234578 Combinations 3
just look at the lack of the killer cage convention
n2 above sums to 14(4) outie
n8 has a 32(5) outie
both of these happen to have no repeated digits
r5 has an outie 14(3) very easy to spot
r1+r2+r3+r4+r5 has an outie 6(1) a single
which leaves an outie 8(2) for r5 to r9
its confined to row 4 and must have no repeated digits so 44 is not in the possibles
when i start getting stumped with a killer i may see n1 with a 2 cell outie
one goes east the other south
outie 4
2 cell cage
4: 13 22
Digits 123 Combinations 2
outie 10
Digit Combinations -
2 cell cage
10: 19 28 37 46 55
Digits 123456789 Combinations 5
outie 18
2 cell cage
18: 99
Digits 9
... by: MK
So the concept of Innies and Outies is this: since any given row, column, or box of nine squares contains the digits 1-9, it must add up to 45 (1+2+3+...+9=45). Therefore, if you have a given set of cells that overlap said row/column/box, plus an extra square (an outie) or minus a square (an innie), you can calculate the value of that square.
Example: a row made up of the followings four cells (the numbers are the sums, underscores is a blank square:
[12 _] [12_] [12_][7_] [_]
[_ _ _][ _ _ _][_ _][_]
The last underscore is part of a two-square cell overlapping the row below. In this case, it's an Innie, because all the other cells are contained in this one row. So you add the sums of the cells: 12+12+12+7=43. You know that the total sum of the row must equal 45. So, 45-43=2 means that the square on the end by itself must be a 2.
It would work the same way for an Outie, except that the total sum of the cells would be greater than 45 and the empty square would be on a different row. (Example: total sum is 48. 48-45=3, so the 3 goes in the Outie square.)
Then you just expand this for multiple rows/columns/boxes. If the sum of one row is 45, then the sum of two rows is 90, the sum of three rows is 135, and so on.
I hope that this helps to clarify. I know that it's hard to visualize when I don't have proper pictures like above.
... by: Kaylea