There is an excellent strategy for Jigsaw Sudoku it is vital to know about - and it uses the odd shapes of the boxes.

Consider the area marked with As in Figure 1. It consists of three cells in the stair-shaped “box”. All the solution numbers for these three cells cannot appear in the cells marked B, since A and B share the top two rows. This means that all As must be in the cells marked C.

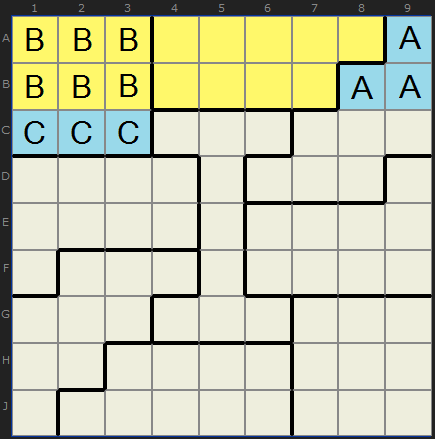
The top two rows are referred to as a “region” while the cells marked C are “leftovers”.

A region can be a single row or column, two adjacent rows or columns (as on the right), or even three or four rows or columns – although there is no significant gains from four or more in a region. A double row or column seems to be the most common, and in such cases the Law of Leftover is as useful as Intersection Removal.

For the Law of Leftovers to work, we want to find a region with an overlapping box – the leftover being the part of the box hanging outside the region. However many cells are left over, we need to find another box that also overlaps our region by the same number of cells. CCC and AAA in Figure 42.1 satisfy this requirement. The examples below should convince you that it’s worthwhile to look out for such patterns.

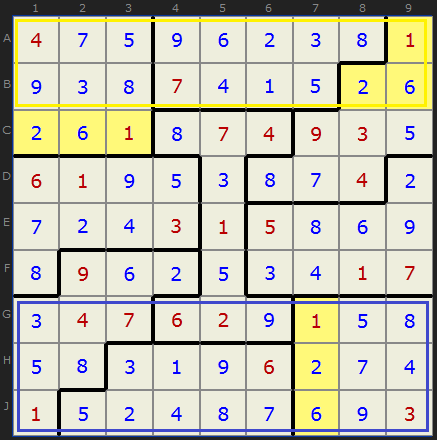
If we examine one possible Sudoku solution for our grid, shown in Figure 2, we can see, as if by magic, that 1/2/6 occupies the areas marked AAA and CCC (areas marked in yellow). That example seems to work. It also works if you take the last two columns on the right.

There is another region at the bottom of the jigsaw – the last three rows marked with a blue ring. Cells F2/F3/F4 contain 9/6/2. The central “I”-shaped box has three cells inside the region; this must be our counter-partner and indeed it contains 6/2/9. This knowledge is going to be very useful.

There are a number of ways to think about this trick. We know that all the numbers in a row, a column or a box always add up to 45, since the numbers 1 to 9 occur once in each unit. If we have a box that is partially within the region, it will contain a certain set of numbers outside the region. In order for the 45 rule to be satisfied for all boxes as well as rows and columns, any deficit must be made up elsewhere – with identical sets of numbers. With two rows or columns, the sum we need to have in mind is 45+45=90. Likewise for three rows or columns, the sum is 135.

The usefulness of this strategy depends on how helpful the design of the jigsaw is. Some jigsaws will be well-suited to it, while others will be very mean, in that you might not find a single instance.

You’ll want to check for LOL occasions just so you don't need to add notes for certain cells. Let’s look at this example of a two-row region at the bottom of the grid. The "outies" are marked in green and correspond to the "innies" in brown. The Law of Leftovers implies that the two numbers in the green cells must be the same two numbers in the brown cells - although it is not possible to know which way round yet,

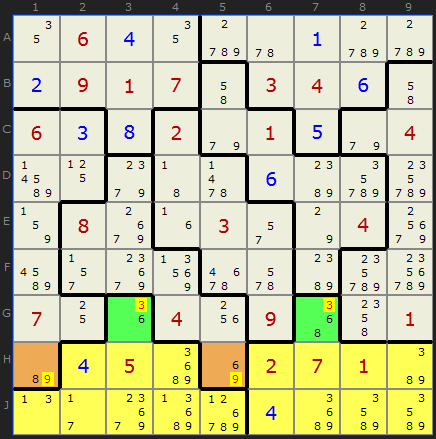
However, we have 3, 6, 8 and 9 as possibles so far. 3 has been eliminated from the brown squares and 9 has been eliminated from the green cells - so these are not candidates for both sets. We are left with 6 and 8 as the only possible solutions for the leftover regions. That's major progress since we get a 6 in G3 and an 8 in H1.

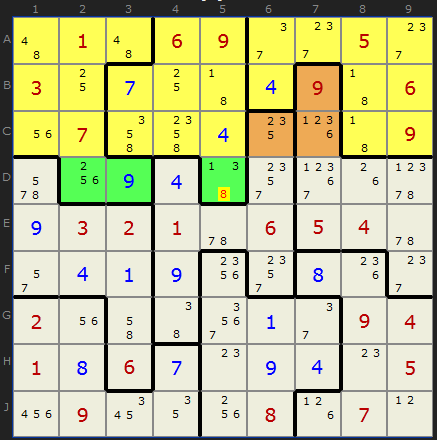
As we saw in the previous example, the leftover region - the bit that sticks out, can be made of cells from more than one shape. The leftover region must be all the cells that stick out (green cells). There will always be an equal number of cells from outside shapes poking in (brown cells).

In this example, three cells marked in green extend out of the top three rows and form the leftover. Three brown cells intrude into the top three rows. We can ask - "what are the common candidates". This tells us that the 8 in D5 can be eliminated.

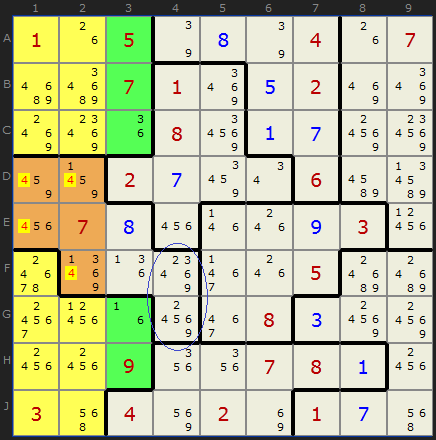
The final example shows a 5-cell left over region. We need five numbers to fill these five cells and column 3 provides them: they must be 3, 5, 6, 7 and 9. Our "innie" area of brown cells has all these numbers, but also a profusion of 4s. They can be removed.

That gives us a a Hidden Pair on 4 in F4 and G4, so we can progress by removing the 4 in E4.