This is a variant of the popular Sudoku puzzle which contains two extra constraints on the solution, namely the diagonals, typically indicated by grey cells. In a normal Sudoku puzzle all rows, columns and 3x3 boxes must be filled with the numbers 1 to 9 without repeating a number. There are nine ‘cells’ in every row, column and box.

In Sudoku X the two diagonals containing nine cells and sharing the central grid cell must also be filled with exactly 1 to 9. The puzzle solver can use this information to reduce the possibilities in those lines and make deductions across the the board previously out of reach in a normal Sudoku. However, these extra constraints allow the puzzle compiler to reduce the number of necessary clues thus creating a balanced puzzle that rivals normal Sudoku in variety and difficulty.

Note, it is perfectly possible to create a normal Sudoku that co-incidentally has the unique 1 to 9 in each diagonal but unless this information is revealed first it is usually of no help to the solver.

In Sudoku X all the normal Sudoku strategies apply - and there are a great number of these. But to complete tough and harder puzzles the solver must be expected to use the extra diagonals. This rule is in proportion to the difficulty. Gentle puzzles should require little to no note taking and can often be solved with normal ‘eye-balling’ techniques. As the grade increases the diagonals contain much more important information.

Some of the basic strategies are illustrated after the examples and show how they can be extended to the diagonals. There are also two examples which show the pitfalls of Uniqueness strategies - and how they do not always apply in the case of Sudoku X.

It is a given to expect Naked and Hidden Pairs, Triples and Quads in the diagonals as you would in any row, column or box. Beyond these are the two types of Intersection Removal. Since the diagonals only ever cross one row or one column at a time the only intersections you should look for are with boxes.

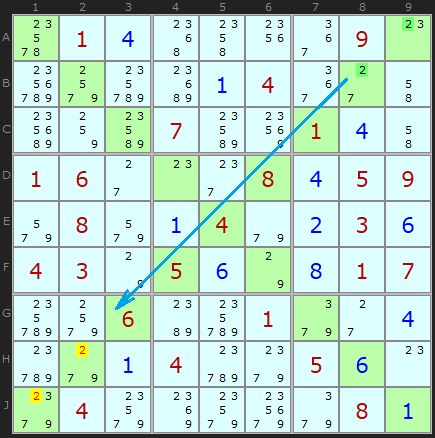
This Sudoku X puzzle I have picked specially for being packed with Pointing Pairs and Box/Line Reductions but example Pointing Pair here is aligned on a diagonal.

The two green cells in A9 and B8 are the only two cells in box 3 with the candidate 2. These align on the diagonal and since 2 must occur on one of the two green cells (we just don’t know which one) it can be removed from anywhere else in the diagonal, namely cell H2 and J1.

There are three simultaneous Box/Line reductions here on numbers 1, 3 and 4. I have highlighted the cells with 1 as a solution or candidate and it is possible to see that the 1s for diagonal 1 (top left to bottom right) exist only in box 1. Therefore A1 or B2 must be a 1 so B1 and A2 cannot be 1. In green is the reduction on Box 5 because of Diagonal 2 (top right to bottom left). Again the 3s only exist in box 5 so the 3s on D4 and F6 can go.

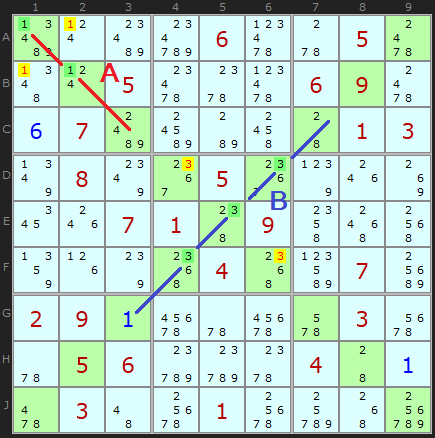
The final reduction is in Box 1 using candidates 4 on Diagonal 1. removing the other 4s in Box 1 gives us a solution of 2 for A2.

The diagonals in Sudoku X afford another line of attack because of the angle they cross the board. Any two cells in a diagonal will share neither the same row or column and are therefore form opposite sides of a rectangle. The other two corners can't contain the same candidate as Pair on the diagonal.

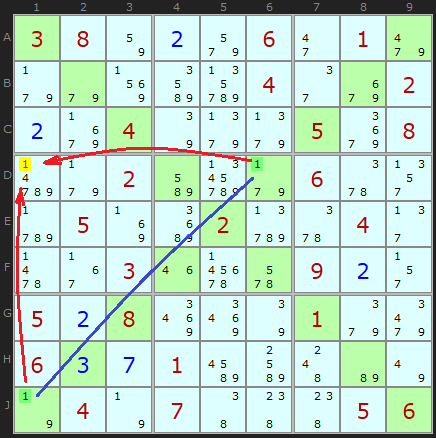
Consider D6 and J1 which are a pair on candidate 1. Either D6 or J1 must be a 1 but they can both see D1 and J6. No 1 can be on either of those cells, thus the 1 on D1 can be removed.

All types of Unique Rectangles can be applied to Sudoku X - but there is a catch!
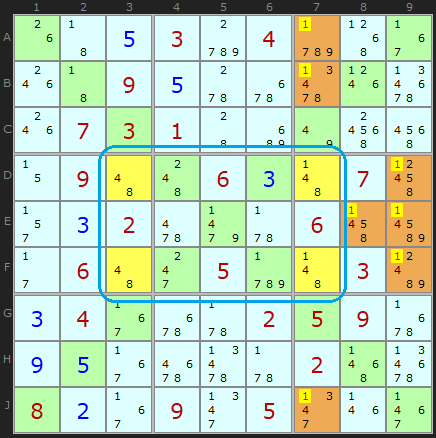
You cannot create the 'deadly pattern' if any of the four cells are on a diagonal.

Remember that the 'deadly pattern' is where you can potentially swap pairs of numbers around and we can make eliminations in order to avoid creating such a pattern. However, if a corner of the pattern is on a diagonal it is not the case that pairs can be swapped around - it would invalidate the diagonal constraint. So we can't use the logic of unique rectangles unless all the cells are away from the diagonals.

This example is rather spectacular - 7 eliminations based on the logic of a Type 2 Rectangle.

Documentation is here.

There is more discussion of the unique properties of Sudoku X on this page.