'The Logic of Sudoku' Resources Page
Introduction
Welcome to the "Logic of Sudoku" resource page.
To start with I have listed the exercises in the book with links to printable versions - in case you'd like to print them out instead of working in the book.
The second set of links are to my Step by Step solver for some of the puzzles and exercises in the book. This, I hope, will allow you to see the examples as the come about. In some cases some strategies might need to be turned off to allow the example to find the use of a particular strategy, but in most cases I have picked examples for the book that are necessary steps.
Any feedback or comments always appreciated.
Andrew Stuart
Corrections
Hidden Pairs - page 20
The sentence immediately under the diagram should read "1 and 5 occur in only two cells in box 2, but they are hidden by the 3 and 8 in C4 and the 3/7/8 in C6". Also the diagram 6.2 should show 1/5 in C4/C6, not 5/8.
Exercise 3 - Hidden Pairs
There is a small error on the exercise answer. One of the Hidden Pairs has been incorrectly highlighted. The fifth one, the {3/9} in box six is the correct Hidden Pair, not the {3/9} in box 8.
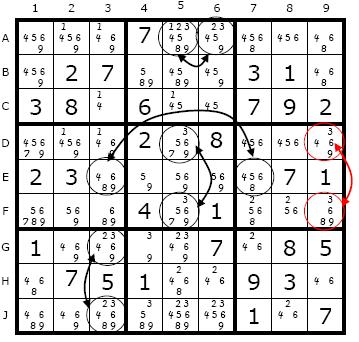
Figure 22.2 on page 63
Unfortunately Figure 12.2 was substituted in place of the actual figure for 22.2. The real diagram is:
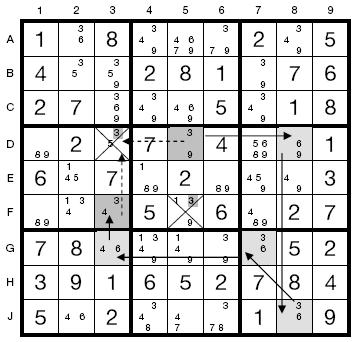
Table on page 123
The Extended Aligned Pair table on page 123 doesn't contain the strikethroughs which remove certain pair combinations and show how 3 can be removed. The corrected table is:

Welcome to the "Logic of Sudoku" resource page.
To start with I have listed the exercises in the book with links to printable versions - in case you'd like to print them out instead of working in the book.
The second set of links are to my Step by Step solver for some of the puzzles and exercises in the book. This, I hope, will allow you to see the examples as the come about. In some cases some strategies might need to be turned off to allow the example to find the use of a particular strategy, but in most cases I have picked examples for the book that are necessary steps.
Any feedback or comments always appreciated.
Andrew Stuart
Printable Exercises
The following are the exercise puzzles in the book. You can click on the links to get a printable version of each puzzle.
- Naked Pairs Quiz
- Naked Quads Quiz
- Hidden Pairs Quiz
- Intersections Quiz
- Simple Colouring Quiz
- Multi-Colouring Quiz
- Y-Wing Chain Quiz
- X-Cycle Quiz
- Grouped AIC Quiz
- Finned X-Wing Quiz
- Empty Rectangle Quiz
- Type 2 Unique Rectangle Quiz
The following are the Sudoku puzzles in the book. You can click on the links to get a printable version of each puzzle or load the puzzle into Andrew Stuarts Step-by-Step solver
- Puzzle No 1 - Load into solver
- Puzzle No 2 - Load into solver
- Puzzle No 3 - Load into solver
- Puzzle No 4 - Load into solver
- Puzzle No 5 - Load into solver
- Puzzle No 6 - Load into solver
- Puzzle No 7 - Load into solver
- Puzzle No 8 - Load into solver
- Puzzle No 9 - Load into solver
- Puzzle No 10 - Load into solver
- Puzzle No 11 - Load into solver
- Puzzle No 12 - Load into solver
- Puzzle No 13 - Load into solver
- Puzzle No 14 - Load into solver
- Puzzle No 15 - Load into solver
- Puzzle No 16 - Load into solver
- Puzzle No 17 - Load into solver
- Puzzle No 18 - Load into solver
- Puzzle No 19 - Load into solver
- Puzzle No 20 - Load into solver
- Puzzle No 21 - Load into solver
- Puzzle No 22 - Load into solver
- Puzzle No 23 - Load into solver
- Puzzle No 24 - Load into solver
- Puzzle No 25 - Load into solver
- Puzzle No 26 - Load into solver
- Puzzle No 26 - Load into solver
- Puzzle No 28 - Load into solver
- Puzzle No 29 - Load into solver
- Puzzle No 30 - Load into solver
- Puzzle No 31 - Load into solver
- Puzzle No 32 - Load into solver
- Puzzle No 33 - Load into solver
- Puzzle No 34 - Load into solver
Corrections
Hidden Pairs - page 20
The sentence immediately under the diagram should read "1 and 5 occur in only two cells in box 2, but they are hidden by the 3 and 8 in C4 and the 3/7/8 in C6". Also the diagram 6.2 should show 1/5 in C4/C6, not 5/8.
Exercise 3 - Hidden Pairs
There is a small error on the exercise answer. One of the Hidden Pairs has been incorrectly highlighted. The fifth one, the {3/9} in box six is the correct Hidden Pair, not the {3/9} in box 8.
Figure 22.2 on page 63
Unfortunately Figure 12.2 was substituted in place of the actual figure for 22.2. The real diagram is:
Table on page 123
The Extended Aligned Pair table on page 123 doesn't contain the strikethroughs which remove certain pair combinations and show how 3 can be removed. The corrected table is:
Table on page 183
In the chapter 44, Killer strategies, is the list of cages with a unique combination of numbers. The correct table is here:
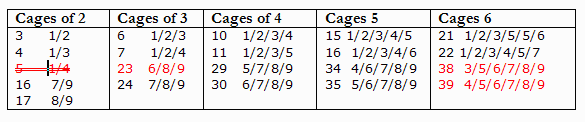
Note: Cages of size 7 were not included since they do not appear in most Killer Sudoku puzzles, but
41 = 2/4/5/6/7/8/9
42 = 3/4/5/6/7/8/9
A full list of all combinations is here: /Killer_Combinations.
If anyone wishes to comment, correct or contribute to these pages please feel free to contact me at andrew@sudokuwiki.org. I'm always interested to hear from other Sudoku fanatics.
Andrew Stuart
In the chapter 44, Killer strategies, is the list of cages with a unique combination of numbers. The correct table is here:
Note: Cages of size 7 were not included since they do not appear in most Killer Sudoku puzzles, but
41 = 2/4/5/6/7/8/9
42 = 3/4/5/6/7/8/9
A full list of all combinations is here: /Killer_Combinations.
If anyone wishes to comment, correct or contribute to these pages please feel free to contact me at andrew@sudokuwiki.org. I'm always interested to hear from other Sudoku fanatics.
Andrew Stuart
Exercise 5 - Simple Chain / Colouring
I've received some emails about the difference between the solver and the solution published as exercise 5 in the book. This diagram to the right is currently how the solver sees the situation.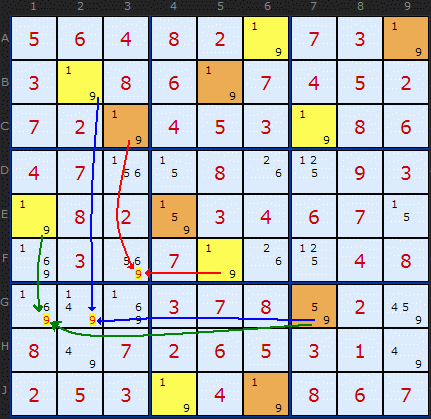
The book shows the elimination at G2 which the solver also shows and I have drawn with blue lines. What is missing from the book solution is the other two eliminations based on different chains. But it must be remembered that Simple Chains and Simple Colouring are two sides to the same coin. The solver uses Colouring to get rid of as many candidates as possible in a single move - but each elimination can be justified by a different chain. The red and green eliminations (and the blue) occur because the 9 can see cells with different colours.
There is a problem with the solution to exercise 5 in that I have only shown one elimination out of a possible three using chains only. That I believe arose because my solver was a more primitive version at the time of writing the book and it wasn't giving me the full picture.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Kwesi
Enjoying your book immensely, and have now reached Puzzle 15 p94. The clue given was that there was an AIC, which I failed to find, I put this into your convenient solver after hours head scratching, and at the point on which I was struggling I came across a Unique Rectangle type 2.
Since I had not come across one of these before, I read all about them in your book. and felt that I had understood them, and so returned back to puzzle 15 for a further head scratching session.
D1&E1 are the floor candidates and contain 4&9 the cells D7 & E7 contain respectively 459 & 46789 to avoid the dreaded pattern at least one candidate 4 or 9 must be removed from either cell E7 or D7 , now I cannot understand why 9 can be removed at E7. All the examples only show 3 candidates at the most in one cell , so how do we know which of the dreaded candidates must be removed.
Thanking you once again for the excellent book and hoping that you can provide me with enough information to bring me back to normality.
Kwesi
... by: Thos
... by: Thos
Also, in the diagram for Exercise 2 on p. 19 some candidate elimination has already been performed, e.g. 6 in F6 by the pair in A6, C6 and 7 in B7 by the pair in F7, H7.
... by: Bizman
... by: Tony Minchin
P12 'dependant' (noun) should be 'dependent' (adjective).
P36 'This clears all [the other] 6s in column 9 ...'
P38 'In Fig 12.3 the sudoku board has, in total, three 5s in three rows..' ?in total, six 5s?
P38 fourth para - '1, 5 and 8 will [have] 5 as the solution..'
p39 The rule 'When there are: only three possible cells for a value..' But p38 at bottom said it could be 2 cells, 3 cells, 2 cells (not just 3,3,3) . And could it also be 3,3,2?
... by: erik niebuhr
I am a beginner in Sudoku, just got your book (logic of S, exellent) but I have a problem with Exercise 2 (Quad, p19): In your answer (p209) you write that the quad of 2/6/7/9 removes the 2 in H2, there is no 2 in H2, it must be the 2 in H1, which means, that 2 should be placed in H3 ?? and thus no quad in row H.
By the way, assuming the quad in column 1, I would remove 2/6/7/9 in B1 (and not only 2/7/9 as you suggest), together with 2 in H2 and 6/9 in J1, correct ?? Kind regards erik (denmark)
... by: Tom Ledwidge
I received your excellent book today and read it cover to cover.
Tom
... by: Marwan Gharaibeh
Hi. I had your excellent book "The logic of Sudoku" and I am proud to say that in addition to the solver on the internet it has helped me reach the highest levels of solving. now the only puzzles I look for are the diabolical, sadistic and develish.
In page 100 , fig 29.3 of your book you talked about the ALS in the figure, but you didn't deal with (2) as a common restricted number for the two sets. in my understanding I see it as common restricted and I don't beleive that your definition applies to it, so why remove the (2)'s from A6 and C6?
May I bother you to respond to this please.
sincerely yours.
Marwan Gharaibeh
United Arab Emirates
In Figure 29.3, 2 is not restricted common. It is present in A4 and C4. Only 1 is restricted common since 1 is the only candidate with the property that is is (a) present is both sets and (b) all occurances can be seen by both sets. Therefore it will be used in one or other set but not both. The 2 in B4 qualifies, but is disqualified by the 2s in A4 and C4 - since these cannot see the other ALS in B6.
Hope that helps
... by: Robert Reily
I have trouble finding the ends of chains. In this example, I can see that one end is G7 as it sees only one other 9 in pair at H9. All others see two. What is the other end and how do you establish that?
Using your solver, it seems that the example has a "9" incorrectly eliminated at F3 and at other places. It seems that this example is messed up based on the solver at Scanraid.
Am I confused is so please help.
Thanks
... by: Richard Kretzschmar
Thanks.
There is a correct way of allocating the + or -. Of the three cells in the second chain two can 'see' the other chains. These are the + cells, which in this case are E8 and J7. G8, the '-' cell can't see any cell in the first chain. To rephase the rule - if some A+ and B+ cells can see each other (which they can and we thus lable them '+') and the A- and B- cells can't see each other (which they can't - and thus we lable them '-') then all N that can see both A- and B- can be removed.
I know at first site it seems chicken and egg, but you looking out for what parts of the chain are visible to parts of other chains.