Exocet
a.k.a. jExocet
Phil's concise description is impossible to better: When 2 of the 3 cells in a box-line intersection together contain 3 or 4 candidates, then in each of the two boxes in the same band but in different lines, if there are cells with the same 3 or 4 candidates, any others can be removed.
I don't intend to duplicate David's work but just the parts implemented by the solver and re-expressed in my own way. Terms and references to the original will be supplied.
Full Documentation Coming Soon
Exocet is a pattern that can often occur in very hard puzzles where the candidate density is very high. With few bi-value and bi-location candidates other strategies give up. Exocet takes on three or four candidate sets at a time which is just what is needed in the bottlenecks of extreme puzzles. My first implementation solved 51 out of 123 of the weekly "unsolvables" that were created by David Filmer. We will be replacing any stock known solvable with even harder puzzles.Phil's concise description is impossible to better: When 2 of the 3 cells in a box-line intersection together contain 3 or 4 candidates, then in each of the two boxes in the same band but in different lines, if there are cells with the same 3 or 4 candidates, any others can be removed.
Order in Strategy List
My instinct is to put this near the end of the Extremes set of strategies but many of the eliminations in Exocet can overlap earlier strategies, I am told. I do not think I have implemented many of those but to test and improve I am putting it at the start of the extremes to give it more exercise. David Bird tells me it can go after the basics but that will have to wait until more variations are in place.Credits
A number of people explored this strategy and its many variations. I am told the name was coined by forum participant Champagne. The pattern was first discovered by Allan Barker in the "Fata Morgana" puzzle[1],[2]. My main source is the excellent JExocet Compendium written by David P Bird, available in fourteen downloadable documents on the EnjoySudoku Forum and David was kind enough to answer questions as well. I would also like to credit Phil's Sudoku Solver as a source of examples and help. Any other credits not mentioned, please email me.I don't intend to duplicate David's work but just the parts implemented by the solver and re-expressed in my own way. Terms and references to the original will be supplied.
The Exocet Pattern
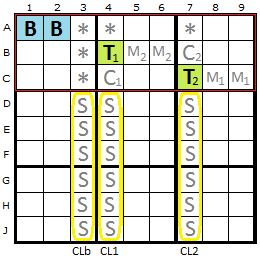
Pattern Rule 1
Two Base cells (B) exist in alignment in one box and usually contain three or four candidates *in total*. That could mean {1,2,3,4} + {1,2,3,4} but could also mean {1,2,3}+{2,3,4} or even {1,2,3}+{3,4}. I've not found an instance of two bi-value cells like {1,2}+{3,4} yet. To be explored.
Pattern Rule 2
We then check if there are two Target cells (T) that contain all the digits of the Base cell (plus any extras). The Targets cannot 'see' each other or the Base Cells. They must also be in the same Tier or Stack (group of 3x3 boxes in a row or column). The diagram highlights the top tier in red. There are only three possible cells for each Target given that they must not be 'seen'.
If Bases and Targets are aligned in a Tier (as in these diagrams) we look for three Cross-Lines that descend from the Targets and the cell not occupied by the Bases. These are marked in yellow - columns 3, 4 and 7. We are interested in the six cells outside the Tier (or stack). These cells are called S-Cells.
We will be talking about some of the other cells in the pattern as well, so lets introduce them. Each Target has a Companion cell marked with a C. Each Target has two Mirror Cells that are next to each opposite Target, marked M1 and M2.
Lastly, the asterisks are called Escape cells which can hold the candidates that are found to be false in the base.
Pattern Rule 3
To be a real Exocet pattern the Companion Cells must not contain the Base candidates, not even as clues or givens.
We will be talking about some of the other cells in the pattern as well, so lets introduce them. Each Target has a Companion cell marked with a C. Each Target has two Mirror Cells that are next to each opposite Target, marked M1 and M2.
Lastly, the asterisks are called Escape cells which can hold the candidates that are found to be false in the base.
Pattern Rule 3
To be a real Exocet pattern the Companion Cells must not contain the Base candidates, not even as clues or givens.
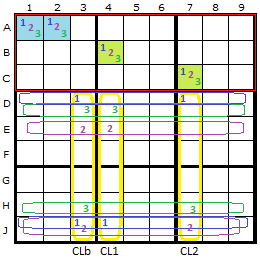
Now one last complication before we can be certain we have an Exocet. In the diagram I've set the Base candidates to be {1,2,3}. There is hopefully a scattering of these in the S-Cells. We want them to appear no more than twice each. If the Cross-Lines are columns we consider the rows where each Base candidate appears. These are called Cover-Lines and I've drawn all the cover-lines in the three colours of the three numbers.
I've stated that cover-lines are perpendicular to cross-lines. Usually they are, but to get the maximum number of elimination rules we can be flexible. It is possible that one Base candidate appears twice only in one column. If we were strictly perpendicular it would require two cover-lines, but all we want to do is "cover" the candidates, so in the single-column case we can "cover" them vertically. So the cover-line = the cross-line.
This will be useful later.
Pattern Inferences
If an Exocet pattern can be confirmed, then following inferences occur:
Note: When we talk about "true Base digits" we are talking about the final solution and knowing what those cells actually contain. We don't know that at the start but eliminations here might tell us more and we can go back through the Exocet check-list.
- The two Target cells must contain different base digits.
- Mirror cells must contain the same base digits as their 'opposite' Target cells together with one digit that is false in the base cells.
- The two true base digits must each be true in two 'S' cells
Note: When we talk about "true Base digits" we are talking about the final solution and knowing what those cells actually contain. We don't know that at the start but eliminations here might tell us more and we can go back through the Exocet check-list.
Elimination Rule 1
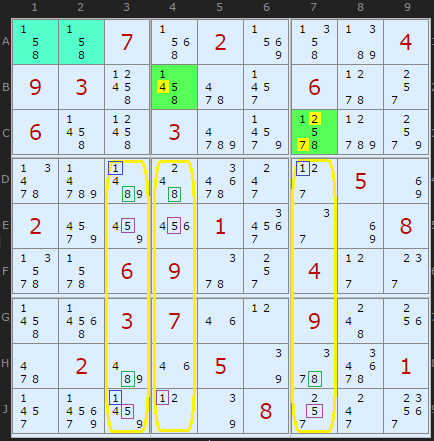
Any candidate in a Target cell that is not one of the Base candidates can be removed. That takes out the 4 in B4 and the 2 and 7 in C7
This example actually contains a whole raft of Exocet eliminations but they rely on another test called the Compatible Digit Check. That I have not implemented so I'm going to ignore those. I will come back to this example in the next update when I've understood this test.
Elimination Rule 3
Bird's definition: A base candidate that is restricted to only one 'S' cell cover house is invalid and is false in the base mini-line and target cells.
Elimination Rule 4
Bird's definition: A base digit in a target that must be true in the other target is false.
Which I take to mean if eliminations thus far reduce one target to one digit ON then it is strongly linked and eliminates like a single.
Which I take to mean if eliminations thus far reduce one target to one digit ON then it is strongly linked and eliminates like a single.
Elimination Rule 5
Bird's definition: A base candidate that has a cross-line as an 'S' cell cover house must be false in the target cell in that cross-line
Elimination Rule 8
Bird documentation states "If a mirror node contains only one possible non-base digit value, it is true in that node and false in the cells in sight of it."
I couldn't make this work without creating incorrect eliminations. By best implementation that doesn't create incorrect removals goes along the lines of "base digit missing from mirror node or base digits missing in the mirrored target cell".
See Tebo below in the comments for more insight.
I couldn't make this work without creating incorrect eliminations. By best implementation that doesn't create incorrect removals goes along the lines of "base digit missing from mirror node or base digits missing in the mirrored target cell".
See Tebo below in the comments for more insight.
Exocet Exemplars
These puzzles require the Exocet strategy at some point but are otherwise trivial.They make good practice puzzles. Klaus Brenner finds.
- Exemplar 1, x1 (score 195)
- More as we find them...

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Sulphur
000400010010305709000090000250040000001200600030009080090060000300008004070000020
https://www.sudokuwiki.org/Double_Exocet
It has deviated from the only example given in the Double Exocet article; the "bases" there align upon rows in their respective boxes, whereas this example highlights dubiously a row and a column, and it has the further misfortune of both appearing within one box. From there it seems to attempt inferring that placing 2/4/6/8 there—either in the real Exocet or in the dubious one—would preclude too many 2/4/6/8 options in the other and removes all of them mutually.
I can believe that 2/4/6/8 are scarce enough in rows B, E and H that the single Exocet notion applies to E1 and H3 in the first stack, and indeed that A5 and C8 cannot be allowed to occupy the Sudoku units covering 2/4/6/8 in other stacks. Clearly though, by inclusion-exclusion we must have B1 and B3 containing the same numbers as E2 and H2, and indeed A2 and C2 matching B5 and B8.
In practice it can be solved quite well from there with chain methods! Treating box 1 as a group junction helps much for that, similar to the idea of double loops, or "SK Loops" as named here. For example, if B8 is not 6 then it is 4, thus E2 becomes 8, thus B5 becomes 2, thus H2 becomes 6—all via the box 1 groups. Either way, H8 therefore cannot be 6, after which 6 becomes unique in column 8 and from there we can solve all four of those cells.
... by: Aleksandra Z
"Suppose there are three critical columns for which three digits can appear only twice each over two bands, due to each digit having two Sudoku units which cover all its possible cells in those bands. By the pigeon-hole principle, the third band must therefore contain those digits once each in those critical columns. A constraint arises if that third band also contains an almost-locked set with the same digits which can see five of the nine critical cells, a large group which therefore may contain no more than one of the digits. The other two digits must therefore appear in the other two pairs of critical cells."
The "Mirror" extension then seems to arise by means of the original columns spanning three stacks and the final two pairs each having one position blocked, creating a braid in the third band. I think the fundamental Exocet logic works without requiring different stacks (breaking "Mirror" logic) and without blocked "Companion" cells necessarily, but going that far would introduce so much box visibility that almost certainly simpler logic would solve the puzzle!
Speaking of which, the Exemplar 1 requires at least Rectangle Elimination to be disabled, and ideally also disable Hidden Unique Rectangle and Aligned Pair Exclusion so that only the Exocet is used.
... by: Tim
So it appears I was initially interpreting "one of them being true" to mean a base digit, rather than one of them having to be true within that s-cell.
... by: Tim
I am hoping someone can clarify what I am missing and/or what part of the clarification of rule 12 from David's compendium means.
Rule 12: For a known base digit, any digit instance that would prevent two of its 'S' cells being true is false.
I understand that, have coded it it my solver and it works,
What confuses me is the last part of the rule 12 clarification: If an 'S' cell is common to more than one base candidate and one of them must be true, any non-base candidates it holds must be false.
I interpret this to mean if a S cell contains one Base digit and one or more Base candidates, any non base candidates are false and can be removed. However, nothing I try prevents incorrect eliminations.
The rule seems simple so I am starting to think there might be something wrong with it.
Maybe my implementation of pattern rules is not quite right but I only have issues (so far) with this rule.
Any ideas?
Note: I can order the solving techniques used by my solver and was testing this puzzle with singles first and exocet second to help more thoroughly test my routines
Here is an example - all singles (done) until it does an JExocet type 12
(my rows and cols are 0-8)
B1 = (2,6,1)
B2 = (2,7,79)
T1 = (0,5,79)
T2 = (1,0,1)
C1 = (1,5,6)
C2 = (0,0,3)
M1a = (1,1,9)
M1b = (1,2,7)
M2a = (0,3,1)
M2b = (0,4,8)
6 is the solution to 4,8 but my solver tries to remove it based on my implementation of the rule 12 clarification.
3 2 4 1 8 79 5 6 79
1 9 7 5 3 6 2 4 8
6 5 8 4 2 79 1 79 3
9 3 2 6 17 5 4 8 17
4 7 5 8 19 2 69 3 169
8 1 6 79 4 3 79 5 2
2 6 3 79 5 1 8 79 4
7 4 9 2 6 8 3 1 5
5 8 1 3 79 4 679 2 679
Thanks
... by: Mike
Mostly because putting a digit on c1 and c2 is the easiest way to remove base numbers as possibilities for those two squares, whilst preserving them as possibilities in the target and S squares.
In fact, I suspect the only other way it can be managed (without destroying the logic of the puzzle and allowing it to be solved via simpler methods) is by overlapping a pair of exocets.
... by: Jorgen Nielsen (Denmark)
I am working on a solver inspired by your own solver.
I have now reached the examples with the Exocet and am testing it on different patterns.
You are looking for more examples, and I have found one with four numbers in the base pair.
Testing on your Fireworks example 1 and unckecking Fireworks in the solver, I found the following pattern:
Exocet pattern of 1247 in base pair I8 and I9 and target cells in G4 and H3
6 removed from G4
9 removed from H3
... by: Ghost 2T
So I still don't fully understand this solution, what kind of hidden & how it works.
Specifically:
- 2 Base cells (158.158) in box 1
- 2 Target cells (158+N) in box (1,2).
- T1 & T2 & B don't see each other
- 2S-cells see T1 & T2 at column 4.7. So where are the S-cells in column 3? Why choose column 3 as S-cells?
- Is the companion cell an opened one or the original one? Is (2,4) in box (2,3) a companion cell? Or force the companion box to be (3,6).
- Similarly, the mirror umbrella too. Is it mandatory to lie close to each other in the same row, or is it okay to lie randomly in the box? Looking at the picture below T1=(158+4) & T2=(158+27), I don't see anything called a mirror box? (r3c89 has no hidden 4, r2c56 has no hidden 27. It's confusing?)
- What are the stars*** cells? is the target cell (158+N) but is not valid?
- Finally, the rule of type 1 I understand. What about the exclusion rules 2,3,... I don't understand what are you talking about?
THANKS!
... by: tebo
060000009020005000008070100007003000830010097000400800004080900000600010500000020
Ruud top50000 Number 12235
After Singles, Pairs, Intersection Reductions, WXYZ-Wing, and Exocet Elimination Rule 3 (your Elimination Rule 1), I get to Elimination Rule 8, which by Bird's definition gives R4C9=1. However, this is inconsistent because the Puzzle solves with R4C9=5.
By definition, a Mirror Node must resolve to one Base Digit and one non-Base Digit. What's missing is that it must be a "True" Base Digit. In the above puzzle, the Base Digits are 2, 5, and 6, however, while examining the pattern, we don't know which are true and which are false. In fact, it's the False Base Digit (R4C9=5) that correctly resolves in the Mirror Node.
While examining the pattern, the only way we can know that a Base Digit is "True" is if previous eliminations reduce the Base Cells to a Locked Pair (I think).
So, Elimination Rule 8 should be something like: After Eliminations, if both True Base Digits are determined, and a Mirror Node contains only one possible non-Base Digit, it is true in that Node and Eliminated from all Cells that See both Mirror Cells, or if the non-Base Digit occupies just one Mirror Cell, it is fixed in that Cell and Eliminated from all Cells that See the Mirror Cell.
All this was probably discussed on The New Sudoku Players' Forum, but I find it too difficult to follow. So, I welcome your critique.
... by: Anonymous
The aim is to find two 'target' cells that will together contain the digits which are in the base.
Say digits A and B are true in the base. In each cross line, A and B must appear once, therefore in the the three cross lines A and B must each appear three times.
Those 3+3=6 instances cannot be in the escape cells as they're seen by the base, they can't be in the companions either due to the pattern definition. So they can only be in targets or S-cells.
There can be only a maximum of 2 S-cell instances as the possible S-cell instances are confined to two cover houses (two instances can't be true in the same cover house) which consequently means that it should appear in at least one target. It can't be true in both targets though as the other base digit would have no target cell to occupy.
Now, the imprtance of mirror cells: Remember that the corresponding mirror pair for a target cell is actually opposite to it. In the example, B4's mirror is C89. We can say that one of the mirror cells (C89) will eventually contain the base digit which will be in the target (B4). The other will contain any other non-base candidate. This is correct because C89 are the only possibles in the box which will be able to contain the base digit, as all the cells in the box are a) seen by the base cells, b) seen by the target, or c) a companion cell.
Also, the target cells seeing each other is perfectly valid as well. In the example the second target C7 could've been in B7, in that case it's mirror should be C56.
So in conclusion, each true base digit must be true two times in S-cells and one time in a target cell, and a mirror cell pair should contain the base digit which is in its target.
Btw, the term 'Exocet' refers to any kind of pattern which has two targets containing two base digits found in base cells. This pattern is a specific case of that, and is called a jExocet (Junior Exocet). This is the most well known Exocet pattern.
... by: Steven
Your solver misses an exocet with base cells A1 A2, targets B4 C7, exactly like the pattern in the first diagram
___
How I understand exocet:
The 3 columns where the S cells are have 2 sections:
1. S cells: has at most 2 of each base candidate
2. not S cells: since the columns require 3 of each base candidate, but the S cells can only supply 2, this section must have at least 1
And there has to be base cells which just happen to eliminate all of the non S cells, *except* the target cells and the companion cells.
But the companion cells don't have base candidates.
So any base digit causes a target cell to have that base digit.
2 base cells, 2 target cells = base cells correspond to target cells
___
I'm not sure why the target cells cannot see each other
It still makes a perfectly valid (base cells correspond to target cells) deduction:
If:
1. 3 lines with 2 sections as described above
--- 1. S cells = not in same tier as base cells and companion cells (max 2 base candidates)
--- 2. not S cells = in same tier as base cells and companion cells (min 1 base candidate)
2. Where base cells limit the second section to 4 cells
3. And 2 of those 4 cells are companion cells (don't have base candidates)
Then:
Base cells correspond to target cells (note that there's no restriction with target cells seeing each other)
___
Or why the target cells must together contain *all* base candidates.
If: All pattern requirements are met, except for a base candidate being missing in the target cells
Then: That base candidate must appear once in the (not S cells) region.
Since that candidate is missing in both the target cells and the companion cells, but still appears in the (not S cells) region, it must see the base cells
So the base cells cannot have that candidate!
So the target cells weren't missing a base candidate after all!
... by: Milten
If a mirror node contains a locked digit, any other digits it contains of the same type (known base or non-base) are false.
A pair of mirror cells must contain exactly one base digit and one non-base digit. That is because they contain the base digit of the opposite target cell, and then the other base digit is eliminated by the neighbouring target cell. So if one of the mirror cells has only base or non-base candidates, we know the other mirror cell will have the other type (base / non-base). Note that we actually don't need a locked digit to use this logic.
Suppose in the example puzzle that the base digits were determined to be 1 and 8 (alternatively, assume the candidate 5 in C9 were eliminated). Then C9 contains only non-base digits, so we may eliminate {2, 7, 9} from C8.
... by: Christopher Eastwood
ER8 says "If a mirror node contains only one possible non-base digit value, it is true in that node and false in the cells in sight of it."
Target Cell F3 contains 234 (which are the three Base candidates), F3's mirror cells (F1 and F2) contain 1279 and 3479 respectively... that's 3 non-base digit values (179), not "only one possible" as ER8 says. So how does ER8 apply?
The mirror cells of F3 are D89, not F12. They contain only {2, 6, 9}, from which it follows that F3 is 2 and D8 is 2.
The elimination follows from the stated Pattern Inference: "Mirror cells must contain the same base digits as their 'opposite' Target cells together with one digit that is false in the base cells." So since 3 and 4 are impossible i the mirror cells, they are eliminated from F3.
I admit that I don't think Bird's Rule 8 gives this. But it sounds like the implementation of Rule 8 more likely correspond to Rules 6 and 7 in the comment below. ("My best implementation that doesn't create incorrect removales goes along the lines of "base digit missing from mirror node or base digits missing in the mirrored target cell".") It sounds like a direct implementation of the Pattern Inference to me.
... by: Anonymous
What I was thinking was some kind of chain hanging off the pattern rather than within the pattern, but didn't come out right.
Certainly going to look closely at the comments when I can get my head into this space again
Cheers
... by: Christopher Eastwood
When running it through this solver (as Simon did in the video), it hits on the Exocet rule twice... the first time, is just eliminating the other candidates from F3 and D7, which is fine.
But the second time is causing me some trouble. The solver mentions using "Elimination Rule 4" (to eliminate 2 from D7) and "Elimination Rule 8" (to eliminate 3&4 from F3). The explanation above doesn't make any mention of either of these rules.
I understood the outcome of ER4 by basically just running through the chain of logic for every possible answer for cell E7, which all eliminate 2 from D7. But I don't understand the logic used for ER8... maybe it's a chain that I just don't have the patience to figure out, but I'm thinking that maybe there is some other application of the rules that makes this make more sense in a simpler/more straightforward way?
Anyway... any help is appreciated.
"I've, hopefully, slightly improved my solver by colouring the cover cells (in yellow) and highlighting the base digits in the cover cells. Might make the Exocet pattern a little more clear. Also, the strategy is visited twice because the second round of eliminations rely on the first Exocet set of eliminations from the target cells (green). P Bird does all eliminations in one step but I insist on separating them since some are knock on effects."
I've also listed the elimination definitions I use and I hope I can expand on them to explain them better. However Exocet documentation is very hard to wade through. There's no chaining as such or knock on chaining.
... by: Anonymous
I think I know how rule 1 works:
The base usually has four candidates for which digit to go in the base cell. If we prove that the two digits in the base cells will be the same as the two digits in the target cells, then we have essentially proved that Rule 1 works, because a foreign candidate cannot exist in the target cells if the base cells have no such corresponding candidate.
Let's say that the base digits are b1 and b2 (these can be any two candidates found in the base cells). Because of this, all the escape cells cannot contain b1 or b2, which creates a massive AIC which removes foreign candidates from the target cells and only leaves base digits.
For example, let us take the example in the article with base digits 1, 5, 8.
Let's say that b1 is 1 and b2 is 5. Then, this AIC is formed:
1[B4] = 5[B4] - 5[E4] = 5[E3] - 5[J3] = 5[J7] - 5[C7] = 1[C7] - 1[D7] = 1[D3] - 1[J3] = 1[J4] -
where "=" is a weak link and "-" is a strong link.
The companion cells and escape cells not having base candidates make sure that the strong links are formed properly, and Pattern rule 4 takes care of the weak links.
If you do have questions please reply. I hope this was clear to everybody
... by: kf4abh
Each of the two target cells in the Exemplar 1's Exocet pattern do not each contain all the base pair candidates, although together they do. So maybe the language of Pattern Rule 2 could be modified: "We then check if there are two Target cells (T) that together contain all the digits of the Base cell (plus any extras)."
I've just discovered the Exocet pattern and think it's great, but I sure would like to know why it works.
... by: PseudoFish
- Base is R3C1 and R3C3
- Target is R1C5 and R2C7
Referring to the samples provided, I get that my Cover Lines would be C257; however, I only get one Cross Link with candidate 8 between the Cross Cover Base and CC1. I cannot make any links to CC2 because it is filled with fixed digits. It looks like I am missing two links for this to work, but somehow SW managed to make this work. What am I missing?
... by: Mist
I just read the article several times to understand the exocet pattern better.
In the only exercise (not including the example in the article) "Exemplar 1, x1 (score 195)" the first (and only) exocet encountered by the solver, does not follow the rules this article teaches us.
Under "The Exocet Pattern - Pattern 2" it clearly says "We then check if there are two Target cells (T) that contain all the digits of the Base cell". However, they don't. So how are we supposed to know that?
The article is confusing in its current state. It would be nice if you could update the article so we could learn more about this very interesting pattern.
Thanks
... by: Mist
I tried the puzzle in the given example: 007020004930000600600300000000000050200010008006900400003700900020050001000008000
Later in the same puzzle, the solver references exocet elimination rule 9. It removes candidate 8 from mirror 2 in row B colum 8. However, I could not find anything on any other exocet rules, so it just left me confused. I would be thrilled if you could include rule 9 (and perhaps rules 2-8 since there being a rule 9 implies there must be rules in-between the rule 1 showed here and rule 9 from the solver).
Thank you
... by: Dale E. Kloss
Cheers
... by: Robert Mauriès
Excuse my English, I'm French.
In your presentation of the exocet you give the result, but you do not give the demonstration.
Where can one find the demonstration of the results of an exocet?