Finned X-Wing
This is a very subtle yet beautiful extension of logic. We're looking at formations that could potentially be X-Wings but have a corner that's not quite right. In an X-Wing we are looking for four cells in a rectangle which contain a candidate N that exists just twice in either the two rows that form the rectangle or the two columns. Our Finned version is still a rectangle but it has extra candidates of the number in question that prevent one of the two pairs we need from existing.
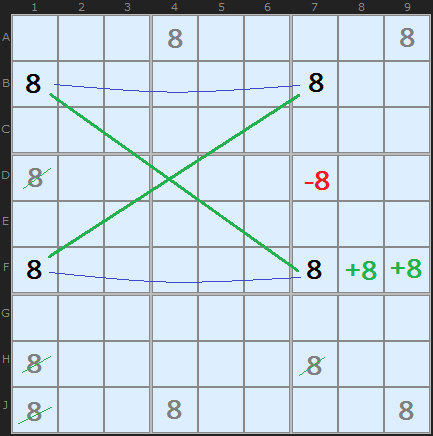
These +8 cells are the 'fin'. The 'fin' or 'fillet' rule goes as follows:
If you can form an X-Wing by ignoring the fin cells, then you can keep your elimination of any cell that shares the same unit as all the cells in the fin.
It's important to remember we can only have one fin at a time!
In our example, the -8 is the only cell that shares a box with the +8 cells. It would have been eliminated anyway if the X-Wing were real. However, none of the other X-Wing eliminations are valid.
In our example, the -8 is the only cell that shares a box with the +8 cells. It would have been eliminated anyway if the X-Wing were real. However, none of the other X-Wing eliminations are valid.
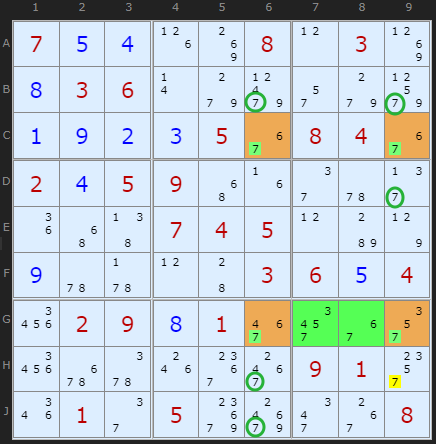
Turning to a real example, consider the potential X-Wing on 7 marked in yellow in Figure 2. We would dearly like to remove all the 7s marked with a green circle. However, there are extra 7s in box 9, marked in green. These are the fin cells. But the fin rule allows us to remove the 7 on H9 at least (red circle).
Turn Grouped X-Cycles off
Sashimi Finned X-Wings
Grouped X-Cycles will be found in the solver before Sashimis so uncheck them to see the examples here.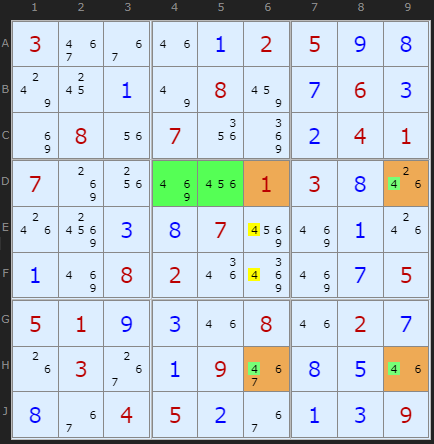
It so happens, that when using the "fin" or 'filleting' rule, it is permissible for the X-Wing to be missing a corner in the finned box. The logic can still be applied! It's going to be fun to explain how and why it works, but first lets look at the example on the right.
We are looking at candidate 4. The fin is again marked in green but the corner of the X-Wing missing. There is no 4 at D6 - which so happens to be a clue, and therefore was never a candidate 4 there at any time! But it doesn't matter, we can remove the 4s from E6 and F6 because they are in the same box as the fin AND in the same column as the odd corner of the X-Wing, H6, in this example.
Where the Finned X-Wing is missing the candidate in the finned box, the type is called a Sashimi Finned X-Wing.
It is possible to consider this example in another way. Either there will be a 4 in D9 or there will be a 4 in one of the two cells {D4,D5}. If the later then the 4s in E6/F6 must go (same box situation) or the 4 in D9 forces a chain giving us 6 in H9 and 4 in H6 - which also eliminates the 4s in E6/F6.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Generalist
... by: Bob
How then do we know if the D4 & D5 are the fibs and we should remove the 4s in cells E6 and F6 as in the example.
Or
If the cells E6 & F6 are the fins when looking at the pattern from the side and we should remove the 4s in cells D4 & D5?
... by: Dawn
First of all, thank you for the amazing site and the work you keep putting in year after year.
I noticed something with the solver, which seems to have been spotted by Anton Delprado earlier as well. Namely, the fact that the solver finds finned x-wing but does not find the corresponding grouped x-cycle, even when the box is ticked. This is the grid with which I spotted this behavior:
https://www.sudokuwiki.org/sudoku.htm?bd=000100000100000000000000004020000000000000000030000000040000003050000002000000000
Interestingly, making the x-wing sashimi does let the solver find the grouped x-cycle(s):
https://www.sudokuwiki.org/sudoku.htm?bd=000100000100000000000000004020000000000000005030000000040000003050000002000000000
Is this intentional, so that the finned x-wing technique does show up even if grouped x-cycles are ticked on? Until now, I usually ticked off ERs and Finned X-Wings because I think they're grouped x-cycles, but maybe I was wrong to do that?
... by: Robert
In the example, the loop is D7-weak-B7-strong-B1-weak-F1-strong-F789-weak-D7
So D7 is at the discontinuity between two weak links, it can be eliminated.
I have to think about whether all finned X-wings are special cases of nice loops with groups.
... by: Kamil
Also I want to thank you for this amazing website.
... by: ElrATiff
Excelent site! Now I'm fully addicted to Sudoku World :)
Some typo in the end of article "Finned X-Wing" (wrong link for Exemplar 1, x1 (score 232)):
there is:
http://www.sudokuwiki.org/sudoku0htm?bd=...
must be:
http://www.sudokuwiki.org/sudoku.htm?bd=...
... by: Orion
"If you can form an X-Wing by ignoring the fin cells, then you can keep your elimination of any cell that shares the same unit as all the cells in the fin."
The only thing that seems to make sense to me when I see these not eliminated would be if I interpreted the rule as follows:
"If you can form an X-Wing by ignoring the fin cells, then you can keep your elimination of any cell (that would be eliminated in a true X-wing) that shares the same unit as all the cells in the fin"
Any clarification you could provide would be appreciated.
Thank you for the Great site.
... by: Ate no basil
For example, in the 4s example, could the fin be in D3 and D4? (rather than D4 and D5)
If that is indeed the case, then in my example we could still eliminate 4s in E6 and F6 (but not if the fin were shifted further left completely into box 4)
... by: Banjo
... by: sean t
In the example, the 7 in J7 and J8 cannot be eliminated because it is possible that G6 contains a 7. If that's the case, then C9 does as well, but none of G7, G8, G9 or H9 do. That leaves only J7 and J8 as candidates for the 7 in box 9. Therefore, the 7 in J7 and J8 cannot be eliminated.
In general, for a finned x-wing, only those cells that can see all the fin cells AND are cells that would be eligible for elimination if it were just a regular x-wing can be eliminated. In this example, without the fin cells present, J7 and J8 would not be eligible for elimination via the regular x-wing.
... by: Anton Delprado
There are no restrictions on Grouped X-Cycles or any other strategy, especially in terms of 'letting through' to any other strategy. However, what I am searching for may be limited to how I search and the generalization I've made. I'll look again at the correspondance to X-Cycles and see if there is something the solver is missing.
... by: David
... by: SueinOz
This site is so amazing! I'm learning so much. A few typos should be expected when your mind is full of all these incredible strategies. My head hurts just reading them!
... by: John Wilcox
... by: chanda
I understand this but which number is safe to remove? I've been testing this and every strategy in a sudoku with an answer key and most strategies are invalid because the answer key has different number than it would be if I used this strategy...
... by: suneet
thanks, love your site
... by: Roland Zito-Wolf
It's worth mentioning that the finned x-wings can be explained as grouped x-cycles of the rule-3 nice loop variety, the kind with 2 weak links in a row.
For example 1, we have C6=C9-H9-[G7,G8,G9]=G6-C6, allowing 7 at H9 to be removed. This clarifies why the 7 at H9 can be removed but not the ones at J7 and J8: only H9 has a link to C9.
The sashimi variation works because it uses exactly the same kind of grouped x-cycle: H9=H6-E4-[D4,D5]=D9-H9 and likewise for F5.
That raises the question of whether the Swordfish and Jellyfish can be related to more general strategies as well...
love your site!