Double Pointing Sets
When it comes to Jigsaw Sudoku, it can't be emphasised too much how important Pointing Pairs and Line/Box Reduction are for candidate removal and general puzzle cracking. They are important for normal Sudoku puzzles but excel in Jigsaws because the shapes allow for many more instances. And not just Pairs and Triples but Quads and upwards.
This extension is very easy to spot - so I have put it before Law of Leftovers in the solver. Experienced Jigsaw solvers are probably using this all the time!
The strategy family of Intersection Sets looks at how rows and columns intersect or overlap with boxes (or shapes in Jigsaw). It is fascinating to know that precisely because Jigsaws are very odd shapes - often elongated, we can improve the one box/one line Intersection Removal technique just for Jigsaws. We can 'double up' using two boxes and two lines (two rows or two columns).
Pointing Pairs and Line/Box Reduction are flip opposites of each other, and same goes for their double versions. Pointing Pairs look for a box containing candidates X that all line up on a row or column. The solution must exist in the box so it excludes X from the rest of the line or column. What if we find two boxes where all the candidates line up on exactly two rows (or two columns)? Then we know any other candidate pointed at can't be the solution.
This extension is very easy to spot - so I have put it before Law of Leftovers in the solver. Experienced Jigsaw solvers are probably using this all the time!
The strategy family of Intersection Sets looks at how rows and columns intersect or overlap with boxes (or shapes in Jigsaw). It is fascinating to know that precisely because Jigsaws are very odd shapes - often elongated, we can improve the one box/one line Intersection Removal technique just for Jigsaws. We can 'double up' using two boxes and two lines (two rows or two columns).
Pointing Pairs and Line/Box Reduction are flip opposites of each other, and same goes for their double versions. Pointing Pairs look for a box containing candidates X that all line up on a row or column. The solution must exist in the box so it excludes X from the rest of the line or column. What if we find two boxes where all the candidates line up on exactly two rows (or two columns)? Then we know any other candidate pointed at can't be the solution.
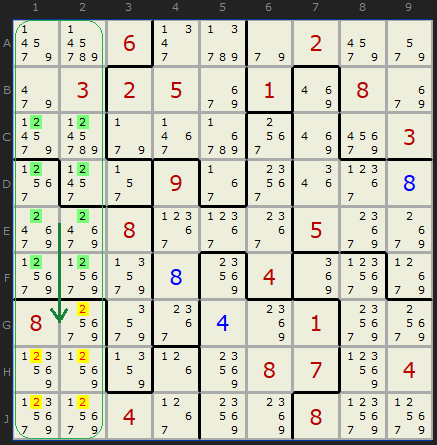
Here is a clear example. All the green highlighted 2s exist in just those two columns AND in just those two shapes. We don't know where in those eight possible places the two solutions for 2 must go - but it excludes 2 from the rest of the columns outside the two shapes. The solve returns:
Double Pointing Set
The two boxes 1 and 4 contain 2 in just columns 1 and 2, so...
- 2 can be removed from H1
- 2 can be removed from J1
- 2 can be removed from G2
- 2 can be removed from H2
- 2 can be removed from J2
It's worth pausing at this point to consider why this doubled up version doesn't work in normal Sudoku. In that puzzle you never get more than three boxes overlapping any row or column - the nine 'shapes' are arranged specifically in that symmetrical way. Take a look at cells H4 and J4. They belong to the shape in the bottom left corner but stick way out into the fourth column. At least two numbers from 1 to 9 must go in there, so whatever they are, they will not be in the rest of the shape. I can tell from the result of this strategy that 2 has been excluded from all the yellow highlighted cells and 4 is a clue in J3. So I am pretty certain 2 will be the solution of one of those two cells. The 2 in B3 satisfies the requirement for column - but is in a completely different shape. These innies and outies that poke into columns and rows don't exist in normal Sudoku, so you'll never get the opportunity for this arrangement except in a Jigsaw puzzle.
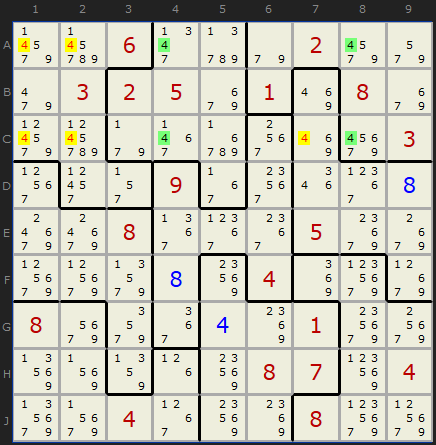
Immediately following the elimination above we get another Double Pointing Set. Not every sequence will be this generous; sometimes only one or two candidates can be removed, but it might save you a more complex strategy down the line.
Double Pointing Set
The two boxes 2 and 3 contain 4 in just rows A and C, so...
- 4 can be removed from A1
- 4 can be removed from A2
- 4 can be removed from C1
- 4 can be removed from C2
- 4 can be removed from C7
I've chosen this puzzle as it contains a good number of normal Intersection Removal and many of the doubled up version. I suggest you run it through the solver from the start.
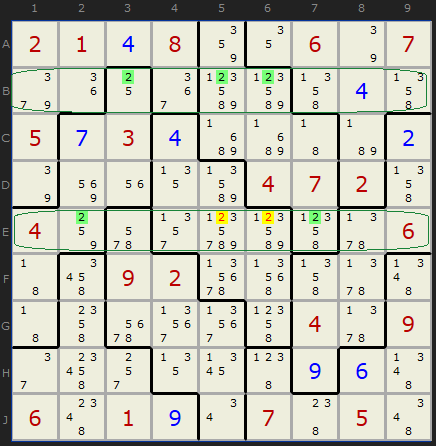
In this example I wanted to show how the two lines do not have to be adjacent. They can be as far apart as the greatest extent of the two boxes (as long as they share rows or columns). In this case there are two rows between. The solver gives this result:
Double Pointing Set
The two boxes 2 and 4 contain 2 in just rows B and E, so...
- 2 can be removed from E5
- 2 can be removed from E6
Again, this is a good example of a "tough" grade puzzle with many Intersection Removals.
By doubling up the first strategy I'm begging the question, can you triple up as well? There is no logical reason why not, but this is rare as it would require five different shapes to intersect in a row or column. It is in the solver.
If you work out an example, please let me know and I'll add it to this page.
Double Pointing Sets are only half the story. Do read the next article on Double Line/Box Reduction for the complete picture.
I am grateful for Brian Hobson for putting me on the track for these strategies. He says he's been using them for years to great success and I agree they are easy to spot.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Doug
- 2 can be removed from J1
- 2 can be removed from G2
- 2 can be removed from H2
- 2 can be removed from J2
If this removal is performed, the lower left corner r(9 squares, G1 to J3) will never contain a value of 2.
... by: Laurence
... by: Brian Hobson
... by: puzzler77